
不確定性限界に迫る超高速時間分解ラマン分光
Abstract
自然科学の原点は自然を観察することにある。自然を観察する手段の進歩は科学の視点を拡げ、より深い自然の理解をもたらす。分光学は自然を原子、分子レベルで観察する最も基本的な手段を提供する。20世紀、とくにその最後の30年の間に、レーザー、エレクトロニクス、電子計算機の技術革新に支えられて、分光学が飛躍的に発展し、それに牽引されて自然科学も大きく進歩した。21世紀においても同様に、分光学の発展は自然科学の進歩を先導して行くであろう。
振動分光学は、分子から生細胞、生体組織に至るまで、分子レベルで物質を解析するための極めて有力な手段を提供する。振動スペクトルが「分子の指紋」と呼ばれるように、分子の個性を鋭敏に反映し、分子の構造、ダイナミクス、またそれらが置かれた環境に関する豊富な情報を含んでいるからである。ラマン散乱によって得られるラマン散乱スペクトル(以下ラマンスペクトルと略す)は、赤外線吸収スペクトルと並んで、振動分光学の実験的基盤を与える。物質を分子レベルで理解しようとする科学、即ち化学にとって、ラマンスペクトルなど振動スペクトルの測定法の高度化は、戦略的に大きな意味を持つ。
分光手法には、それぞれに特有な原理的限界がある。多くの分光学者が、これらの限界に迫る極限的分光法の開発に向けて不断の努力を重ねてきた。本稿では、筆者らが「時空間における振動スペクトル測定の極限化」という主題のもとに進めてきた新しい測定法開発の一例として、不確定性限界に迫る超高速時間分解ラマン分光について概説し、化学測定の確度、精度、感度の向上とそれによって先導される化学研究の進歩について具体的に考えてみたい。
フーリエ変換限界
量子力学の不確定性原理として知られているように、時間とエネルギーの確度を同時に無限に高くすることはできない。分光学の観点から言えば、レーザーパルスの時間波形とスペクトル波形の間には、フーリエ変換の関係があり、時間幅とスペクトル幅を同時に無限に小さくすることはできない。その結果、時間幅の短いレーザーパルスを用いてスペクトルを観測すると、スペクトルがぼやけてしまい、スペクトル分解能が低下する。この関係をsinh2の時間パルス波形を仮定した理論曲線で表わすと図1のようになる。このパルス波形の場合、ピコ秒(ps)単位で表わしたパルス幅Δtと、波数(cm-1)単位で表わしたスペクトル幅Δνの積は、10.5 ps cm-1より小さくなることができない。時間およびスペクトル分解能の目安としてパルス幅をとって考えると、1 psの時間分解能を要求した場合、スペクトル分解能は10 cm-1に低下し、逆に1 cm-1のスペクトル分解能を要求した場合、時間分解能は10 psに低下する。通常、凝縮相のラマンスペクトルに現れるバンドは、振動の位相緩和時間の逆数に対応して数 cm-1の幅を持つ。したがって、凝縮相のラマンバンドの幅と同程度のスペクトル分解能で、本来のバンド形を大きく損なうことなくラマンスペクトルを観測しようとすると、実現し得る最高の時間分解能は数 psということになる。
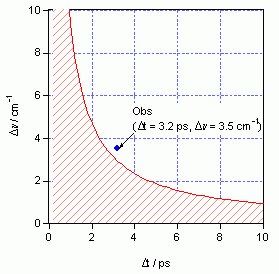
図1: sinh2の時間波形をもつピコ秒パルスのパルス幅ΔtとΔνの関係。不確定性原理により実現不可能な領域を斜線で示してある。青い丸●は図3に示すシステムで実現された時間幅とスペクトル幅を表わす。
ポンプ・プローブ時間分解ラマン分光
光によって分子を励起し、励起状態から生成するさまざまな過渡分子種のラマンスペクトルを、時々刻々時間を分解して測定することにより、化学反応の素過程を詳細に調べることができる。このような手法を、ポンプ・プローブ時間分解ラマン分光法と呼ぶ。この手法では、基底状態にある分子を、ポンプレーザーパルスによって文字通り励起状態へ汲み上げ、生成した過渡分子種のラマンスペクトルを、プローブレーザーパルスを用いて測定する(図2)。ポンプパルスとプローブパルスの時間間隔(これを遅延時間という)を変化させることによって、時間を分解したスペクトル計測を行う。
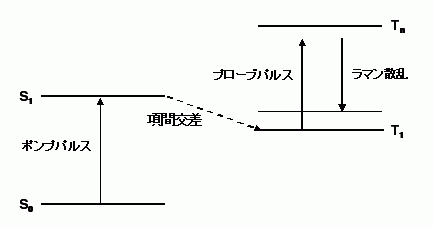
図2: ポンプ・プローブ時間分解ラマン分光の概念図。ポンプパルスによって、分子を基底状態(S0)から第一励起1重項状態(S1)へ励起し、項間交差によって生成した最低励起3重項状態(T1)のラマンスペクトルを観測する場合を例にとってある。Tn←T1吸収と共鳴した波長を持つプローブパルスを用いている。
プローブパルスに要求される特性
ラマン散乱の断面積は極めて小さい。非共鳴条件下では通常10-30 cm2から10-35 cm2 程度である。そのため、観測可能な散乱光子数を得るには、mW以上の平均出力が必要である。波長500
nm、平均出力1 mWのレーザービームを、レンズで100 μmΦに絞り込むと、3x1019 光子cm-2 s2の光子フラックスが得られる。分子量100、密度1
g cm-3の仮想的分子からなる試料を考えよう。直径100 μm、長さ1 cmの試料中に含まれる分子の数は約5x1017個であり、これらの分子により散乱される光子数は毎秒102から107のオーダーとなる。CCD検出器を用いれば、この程度の光子数の散乱光信号を高いS/N比で検出することは容易である。共鳴条件下では、ラマン散乱の断面積が数桁増大するが、レーザー光の吸収を避けるために試料の濃度を数桁下げなければならないので、mW以上の平均出力が必要であるという事情は変わらない。
ピコ秒パルス中の光子は短時間に集中して試料分子に到達する。パルスエネルギー1 mJ、パルス幅1 psのレーザーを100 μmΦに絞り込むと、その光電場は1010
V m-1にも達する。このような強い電場下に置かれた試料は容易にプラズマ化し、いわゆる誘電破壊を引き起こしてしまう。また、強い光電場によって、様々な非線形光学過程が起こり、ラマン散乱の観測を妨害する。したがって、同じ1
mWの平均パワーのレーザーでも、繰り返し率の小さなパルスレーザーはラマン分光の光源としては適さない。
ポンプレーザー光の試料への侵入長を確保し、光励起によるポンピングを効率良く行うために、光学密度を1ないし10程度に抑える必要がある。モル吸光係数104の試料分子では、濃度を10-3ないし10-4mol
dm-3程度に抑えなければならないことになる。そのため、生成した過渡分子種のラマンスペクトルを観測するためには、共鳴効果による散乱断面積の増大を利用することが不可欠になる。したがって、プローブレーザーの波長は観測する過渡種の電子吸収波長と一致するように選ぶ必要がある。例外を除いて、時間分解ラマン分光は、厳密には時間分解共鳴ラマン分光(Time-resolved
Resonance Raman Spectroscopy; TR3)と呼ぶべきものである。
ポンプパルスに要求される特性
光励起によって、短寿命過渡分子種をラマン分光によって観測するのに十分な濃度で生成させるためには、ポンプパルスの1パルスあたり1 ?J程度のエネルギーが必要である。波長250 nm、パルスエネルギー1 μJ、パルス幅1 psのレーザーを100 μmΦに絞り込むと、約1028光子/sの光子フラックスが得られる。強い許容電子遷移の吸収断面積は10-16 cm2程度である。このパルスレーザーで吸収断面積10-16 cm2の分子を光励起すると、1012 s-1の励起速度が得られる。即ち、1psのポンプパルスが照射されている間に、平均で分子は1回光励起されることになる。
フーリエ変換限界ピコ秒時間分解ラマン分光装置
筆者らは、図3に示すピコ秒時間分解ラマン分光装置を製作した[1]。フーリエ変換限界に迫る時間分解能(図1中の青丸)を実現し、かつ高いS/N比で光励起過渡種のラマンスペクトルを観測することを目的としてこの装置を設計した。上述したポンプおよびプローブレーザーパルスに要求される特性を満たすために、繰り返し率の高い(2
kHz)のピコ秒レーザーシステムを用いた。このレーザーシステムでは、モードロックNd:YAGレーザーを基本として、その出力を色素増幅器で増幅する方式を採用した。色素増幅器の励起源としては、モード同期パルスを種としたNd:YAG再生増幅器を用いた。Nd:YAGレーザーから出力されるモード同期ピコ秒パルスの波長は1064
nm、時間幅は約100 psであった。この出力を光ファイバーと回折格子によって5 psまで圧縮した後、第2高調波(532 nm)に変換し、色素レーザーを同期励起した。このように、一度パルス圧縮した光で色素レーザーを同期励起することによって、フーリエ変換限界に近いピコ秒パルスを得ることができた。同期励起色素レーザーからの出力を、色素増幅器によって約104倍に増幅した。色素増幅器からの出力パルスの特性は、波長588
nm、パルスエネルギー10 &mn;J、繰り返し率2 kHz、パルス幅3.2ps、スペクトル幅3.5 cm-1であった。これの第2高調波をとることによって、波長294
nm、パルスエネルギー1 μJ、繰り返し率2 kHz、パルス幅2.2 psのピコ秒紫外パルスを得た。これをポンプパルスとして用いた。また、第2高調波発生の際に未変換のまま出てくる588
nmのパルスをプローブパルスとして用いた。プローブパルス光の光路には、光学遅延回路とNDフィルターを置いた。光学遅延回路により、プローブパルスに適当な時間遅延を与えることができる(1
psは0.3 mmの距離に相当する)。NDフィルターによって、ポンプパルスエネルギーを調節することができる。
このNd:YAGレーザーシステムは、ピコ秒時間分解ラマン分光の光源として理想的な時間特性を有しているが、ポンプ光の波長がプローブ光の波長の1/2で固定されるという制限がある。Ti:Sapphire再生増幅器とパラメトリック増幅器を用いた波長可変ピコ秒レーザーシステムでは、ポンプおよびプローブ波長を独立に選択することができる。しかし、パルスの時間幅とスペクトル幅の積が、フーリエ変換限界の数倍あり、時間分解能とスペクトル分解能の極限化という観点ではNd:YAGレーザーのシステムに及ばない。
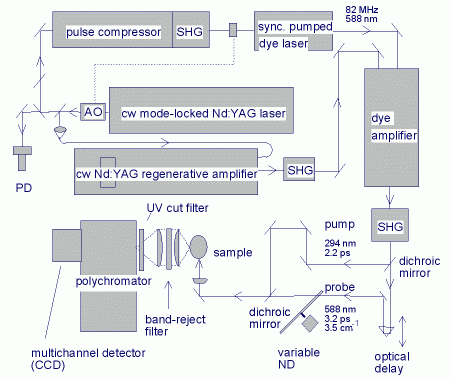
図3: ピコ秒時間分解ラマン分光装置のブロック図
ポンプ光とプローブ光は2色性平面鏡で同軸に重ねられた後、フィルム状ジェットとして噴出された試料溶液に集光される。ラマン散乱光は凸レンズで平行光束に変換され、フィルターでレーリー散乱光や乱散乱光が取り除かれた後、f数の整合をとった凸レンズで分光器(回折格子多色器、polychromator)の入り口スリット上に決像され、分光されてCCD検出器で検出される。この集光過程で、信号として検出される散乱光子数は、もとの1/100程度に減少する。ラマン散乱は球面波として4πradの立体角で射出されるが、実際に集光されるのは1 rad程度であり、散乱された光子の約1/10しか集光されない。積分球のような装置を用いて4πradの立体角で集光することは可能であるが、ラマン分光の大きな特徴の一つである偏光測定が不可能になる。レンズやフィルターでの反射損失は、光学素子1枚あたり10%程度であり、集光系での反射による損失は数10%になる。この損失は、反射防止コーティングによって最小化することができるが、使用波長が限定される。回折効率の高いホログラフィック回折格子を用いれば、分光器のスループットを50%近くまで向上させることが可能である。また、CCD検出器の量子効率は、波長によっては90%を超え、これ以上の大幅な改善は望めない状況にある。結論として、使用波長を限定するなど特化した設計を行わない限り、図3に示した方式のラマン散乱光の分光検出系を大幅に上回る検出感度を実現することは原理的に不可能である。
S1trans-スチルベンのラマンスペクトルと光異性化反応
ピコ秒時間分解ラマン分光を用いて、筆者らが長年にわたって研究している系の一つが、図4に示すS1trans-スチルベンの光異性化反応系である[2]。
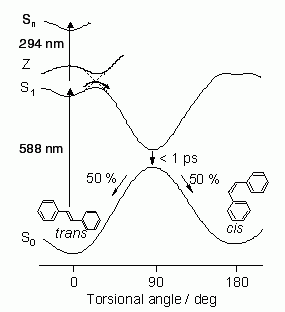
図4: Trans-スチルベンの光異性化反応の反応経路
スチルベンは、基底電子状態でtrans型(内部回転角0°)とcis型(内部回転角180°)の幾何異性体を持つ。2つの異性体を隔てるポテンシャル障壁が十分高いので、室温でtrans型がcis型へ熱的に変換されることはない。しかし、trans型を紫外光で光励起すると光異性化反応によってcis型が生成する。この反応の経路は、多くの実験的、理論的研究によって明らかになっている。即ち、光励起によって生成したS1
trans-スチルベンは、溶媒に依存した30から200 psの時定数で内部回転角が90°のねじれ型に異性化し、1 ps以内にそのねじれ型を保ったのままS0状態に戻り、最終的に約1:1の比でtrans型とcis型を与える。しかし、S1状態で何故(S0状態では起こらない)中央の炭素-炭素結合回りの回転が起こるのか、またどのようなきっかけで、どのような時間スケールでこの回転が起こるのかなど、肝心な点は全く不明である。このような事情は、溶液中の化学反応一般にあてはまる。溶液中の化学反応の微視的機構は全くわかっていないと言ってよいのが現状である。そこで筆者らは、trans-スチルベンの異性化反応をモデルとして、反応の起こる現場であるS1状態のラマンスペクトルを観測することにより、溶液中の化学反応の微視的機構について新しい知見を得ることができないかと考えた。
図3のピコ秒時間分解ラマン装置は、S1trans-スチルベンのラマンスペクトルを測定するために最適化したものであり、294
nmのポンプ光で効率良くtrans-スチルベンをS1状態に励起し、588
nmのプローブ光でSn←S1遷移と共鳴した共鳴ラマンスペクトルを観測することができる。クロロホルム溶液中のS1trans-スチルベンのラマンスペクトルを図5に示す。
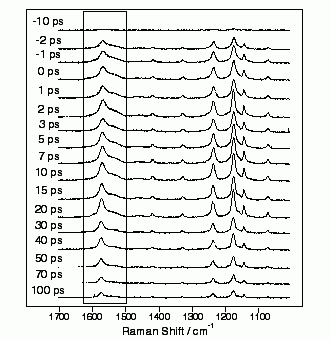
図5: クロロホルム溶液中のS1trans-スチルベンのピコ秒時間分解ラマンスペクトル
波数1000から1700 cm-1の領域に7本のラマンバンドが高いS/N比で観測されている。ここでは枠で囲んだ1570 cm-1のバンドに注目する。13Cや2Hなどの同位体効果から、このバンドがS1trans-スチルベンの中央の炭素-炭素伸縮振動に由来することが明らかとなった。1570 cm-1という波数は、この炭素-炭素結合が2重結合であることを示している。理論計算から、S1状態ではtrans-スチルベンの中央の炭素-炭素結合が単結合的になっていて、その結果容易に回転が起こり、異性化が進行するとする説が提出されていたが、ピコ秒時間分解ラマン分光の結果は、この説を明確に否定した。ではS1状態ではどのような機構で2重結合の回りの回転が起こるのだろうか?その謎を解き明かす手掛かりが、のC=C伸縮バンド形の溶媒および温度依存性の解析から得られた。
C=C 2重結合バンド形の時間および溶媒による変化[3-5]
図5からもわかるように、C=C伸縮バンドのピーク位置とバンド幅は時間とともに変化する。この時間変化を拡大して示したのが図6である。ピーク位置は時間の経過とともに高波数にシフトし、バンド幅は減少する。このような小さなしかし有意なラマンスペクトルの時間変化の検出は、図3に示したフーリエ変換限界のピコ秒時間分解ラマン分光装置ではじめて可能になったものである。試料溶液の温度を変化させた実験、およびStokes散乱とAnti-Stokes散乱の強度比の測定から、このスペクトルの時間変化は、光励起によってS1trans-スチルベン分子に与えられた余剰振動エネルギーによる系の温度上昇と、その後の冷却過程に由来するものであることがわかった。その詳細については報文[6]に譲りここでは立ち入らない。
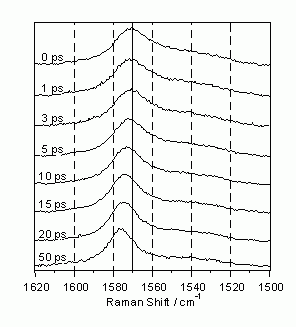
図6: S1trans-スチルベンのC=C2重結合バンド形の時間による変化
先に述べたように、trans-スチルベンのS1状態から90°ねじれ型への異性化反応は、顕著な溶媒効果を示す。したがって、異性化反応の微視的機構がラマンスペクトルに反映されているとすれば、それは溶媒によるスペクトル変化として現れるに違いない。振動冷却に由来するC=C2重結合バンド形の時間変化は、励起後50 psで完了する。そこで、振動冷却の影響を取り除いて、真の溶媒効果を調べるには、励起後50 psの時間分解ラマンスペクトルを溶媒を変えて観測すればよい。図3の装置の時間分解能は3 psであるから、このような測定は十分に可能である。溶媒をヘキサンからヘキサデカンまで系統的に変化させたときの励起後50 ps におけるC=C2重結合バンド形の変化を図7 に示す。溶媒がヘキサンからヘキサデカンに換わると、同じ無極性溶媒であるにも拘わらず異性化反応速度は70 ps-1から130 ps-1へと大きく変化することが知られている。図7のC=C2重結合バンド形の変化をこの速度変化と定量的に関係付けることができれば、異性化反応の微視的機構についての手掛かりが得られるはずである。
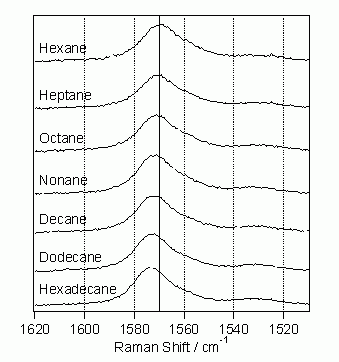
図7. S1trans-スチルベンC=C2重結合バンド形の溶媒による変化
溶媒誘起動的分極と振動バンド形
溶液中の分子振動数は、溶媒との相互作用によって時々刻々、確率論的に変動している。この振動数変動は、振動の位相緩和を引き起こし、結果として振動バンド形を決める要因となる。筆者は、溶質と溶媒の相互作用を、溶媒の作る電場の揺動による溶質の電子分極(溶媒誘起動的分極)として捉え、振動数の確率論的変動をモデル化することにより、溶媒場の揺動と振動バンド形を結び付ける式を導出した[7]。図8に示すように、3段階で振動数の変動をモデル化して理論を構築した。
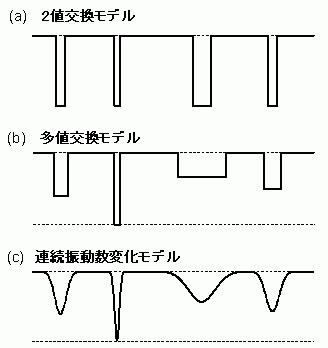
図8: 溶媒誘起動的分極による溶質分子の振動数の確率論的変動のモデル
まず最も単純な2値交換モデル(図8-a)から始める。このモデルでは、S1trans-スチルベンの中央の炭素-炭素伸縮振動数が、C=C2重結合に対応する振動数ω1と、C+-C-単結合に対応する振動数ω2の2つの値を確率論的に往復すると考える。
|
(1) |
ここでW1は、ω1がω2に転移する平均速度、W2はそれが元に戻る過程の平均速度である。即ち、1秒間にW1回、溶媒場の揺動によってC=C2重結合がC+-C-単結合に分極し(溶媒誘起動的分極)、平均1/ W2秒後に元に戻る。この分極を考慮することは、S1状態と近接して存在すると考えられている対イオン状態z(図4参照)の異性化への寄与を取り入れることであり、断熱近似ではS1状態とz状態の混合によるavoided crossingを考えることに相当する。
2値交換モデルで、W2>>W1かつ(ω1-ω2)/W1<<1が成立する非対称極限に注目する。即ち、炭素-炭素伸縮振動数は殆どの時間ω1であり、時々ω2に転移するがすぐに元に戻り、ω2に転移したことによる位相のズレは1に比べて十分に小さい場合を考える。後に述べる実験との一致から、この条件は溶液中のS1trans-スチルベンの動的分極によく対応していると考えられる。筆者はこの条件のもとでは、炭素-炭素伸縮振動バンド形がピーク位置ω1+Δω、バンド幅Γ0+ΔΓのローレンツ形で与えられることを示した[7]。ここで、ω1およびΓ0は分極が起こらない状態でのピーク位置とバンド幅、ΔωとΔΓはそれぞれ動的分極によって生じるピークシフトとバンド幅の増加であり、次のように表わされる。
| Δω = W1τ/(1+τ2) | (2) | |
| ΔΓ = W1τ2/(1+τ2) | (3) |
ここで、τ=(ω1-ω2)/W1は1回のω1からω2への転移によって引き起こされる位相シフトの平均値を表す。また、表式(2)と(3)は、ΔωとΔΓの間に線形関係が成立すること示している。
| ΔΓ/Δω = τ | (4) |
次に、部分的に分極した状態CΔ+-CΔ-を考慮して、ω1とn-1個のωk(k=2,n)の間の交換を考慮した多値交換モデル(図8-b)に進む。ただし、振動数の転移は必ずω1とωkの間で起こるものとし、ωk同士の間では起こらないものとする。つまり、溶媒の揺動による振動数転移がそれぞれ独立に起きる、したがって、一度必ずω1に戻った後、次の転移が起こると考える。そうすると、ピークシフトΔωとバンド幅の増加ΔΓを数学的に厳密に求めることができる[7]。
ここで、W1はω1から任意の他の振動数へ転移する平均の速度、W1kはω1からωkへ転移する平均の速度であり、W1=ΣW1kの関係にある。また、τkはω1からωkへの転移に伴う平均の位相シフトであり、τk =(ω1-ωk)/Wk1で表わされる。Wk1はωkからω1へ戻る平均の速度である。もしWk1が振動数差ω1-ωkに逆比例する(大きな振動数変化を伴う転移は短い時間でもとに戻る)と仮定し、Wk1 =1/τ(ω1-ωk)と置けばτk =τとなり、式(5)と(6)は、(2)と(3)それぞれに帰着し、したがって式(3)も成立する。
より一般的な連続的振動数変化(図8-c)の場合には、上記2つのの交換モデルのように数学的に厳密な取り扱いを行うことができない。しかし、(5)と(6)で示されるように、もしそれぞれの振動数転移が独立に起こると仮定してよい場合には、バンド形は転移による位相シフトのみで決まるので、次のような関係が成立するものと考えられる。
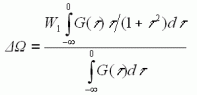 (7)
(7)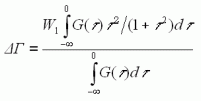 (8)
(8)ここで、G(τ)は、振動位相シフトの分布関数であり、溶媒場の揺動による振動数変動により、特定の大きさの位相シフトがどのような頻度で起きるかを表わす関数である。もしG(τ)の関数形が一定と見做せる場合には、ΔωとΔΓは比例関係にあり、式(4)に類似の式が成立する。振動位相シフト分布関数G(τ)として、ガウス型関数を考える。
| G(τ)=exp(-ln2τ2/τ1/22) | (9) |
ここでτ1/2 は、ガウス型関数の半値幅である。関数(9)を用いて(7)と(8)を数値積分すると、τ1/2 <0.5の範囲で次式が近似的に成立することが示される。
| ΔΓ/Δω=τ1/2 | (10) |
この式は、式(4)の平均位相シフトτの代わりに、ガウス型位相シフト分布関数の半値幅τ1/2が入った形をしている。
以上の考察から、類似した溶媒中、一定の温度範囲で一定のガウス型位相シフト分布関数を考えることができる場合には、動的分極の頻度W1に比例してピーク位置が変化し、またバンド幅もW1に比例して増大することがわかった。図9に動的分極によるバンド形の変化の例を示す。
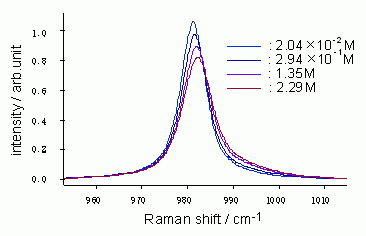
図9: 水溶液中の硫酸イオンのSO対称伸縮ラマンバンド形が示す濃度変化[8]。動的分極モデルの非対称極限として、この変化を定量的に解析することができる。
このとき式(10)が示すように、ΔωとΔΓの間に線形関係が成立する。逆に、実験的に観測されたΔωとΔΓの間に線形関係が見出されれば、動的分極モデルの非対称極限としてバンド形の変化を解析することの合理性が裏づけられ、かつ式(10)を用いてτ1/2の値を実験的に求めることができる。
S1trans-スチルベンのC=C2重結合バンドを、3種の溶媒中(ヘキサン、オクタン、デカン)、268
から338 Kの温度範囲で測定し、得られた40組のピーク位置ωとバンド幅Γをプロットすると図10のようになる。
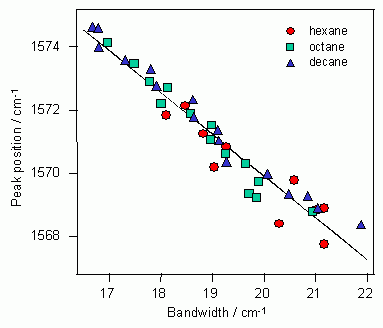
図10: S1trans-スチルベンのC=C2重結合バンドピーク位置ωとバンド幅Γの関係
3種のアルカン溶媒中、268 Kから338 Kの温度範囲で、ピーク位置の変化Δωとバンド幅の増加ΔΓが線形関係にあることが明瞭に示されている。図10の40点の観測値を直線に回帰させ、その傾きからτ1/2の値を求めると0.35となる。式(9)の位相シフト分布関数でτ1/2=0.35 とおき、式(7)を数値積分してピーク位置ωを計算すると次の式が得られる。
| ω=ω0-0.21W1 | (11) |
このようにして、動的分極モデルの非対称極限としてバンド形変化を取り扱うことにより、S1trans-スチルベンのC=C2重結合バンドのピーク位置ωと、動的分極の頻度W1とを関係付ける表式が得られた。すぐ後で示すように、ω0の値を実験的に決めることができ、ω0 =1577.4 cm-1が得られる。この値を用いて式(11)からW1を求めると表1のようになる。
| 283K | 293K | 298K | 303K | 313K | |
|---|---|---|---|---|---|
| ヘキサン | 5.4 | 6.4 | 6.8 | 7.3 | 8.2 |
| オクタン | 4.2 | 4.9 | 5.3 | 5.7 | 6.4 |
| デカン | 3.4 | 4.2 | 4.6 | 4.9 | 5.7 |
即ち、S1trans-スチルベンのC=C2重結合の動的分極の頻度W1は、同一の溶媒では温度が上昇するとともに増大し、同じ温度ではヘキサン、オクタン、デカンの順に小さくなることを示している。これは、巨視的な粘度の示す傾向とよく対応し、W1が溶媒の「動きやすさ」と関係していることを示唆しており、物理的に極めて妥当な傾向である。W1の値は、313Kのヘキサンで最も大きく8.2 ps-1であり、283Kのデカンで最も小さく3.4 ps-1である。即ち、S1trans-スチルベンのC=C2重結合は、溶媒、温度に依存して、1ピコ秒に3から12回の割合で動的に分極している。
溶媒誘起動的分極と異性化反応
図11は、3種のアルカン溶媒中、283Kから313Kまで5つの温度で測定したS1trans-スチルベンのC=C2重結合バンドのピーク位置ωを、蛍光寿命測定から独立に求めた異性化反応速度kisoに対してプロットしたものである。ωとkisoの間に極めて特徴的な相関があることがわかる。図中の回帰直線から明確なように、それぞれの温度でのピーク位置ωと異性化反応速度kisoは比例関係にある。また、5本の回帰直線がkiso=0の極限で1点に交わり、kiso=0でのωの値は温度によらず一定となる。このようなωとkisoの相関は、既存のどの理論でも説明できない全く予想外のものであった。しかし、以下に述べるように、動的分極理論を用いれば極めて明快に説明することができる。
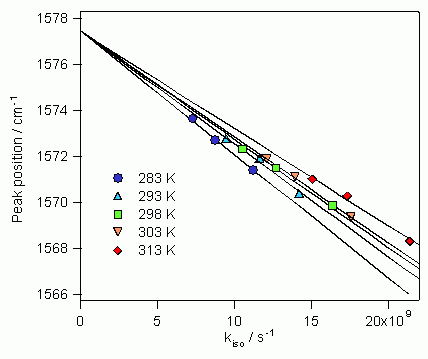
図11:S1trans-スチルベンのC=C2重結合バンドのピーク位置ωと蛍光寿命測定から実験的に求めた異性化反応速度kisoの関係
動的に分極した2重結合は単結合性が増加し、内部回転しやすくなると考えられる。そこで、異性化反応速度が、動的分極の頻度に比例すると仮定し、kisoとW1の間に次の関係が成立すると考える。
| kiso =W1P(T) | (12) |
ここでP(T)は温度に依存する比例係数である。式(12)を(11)に代入するとωとkisoを結び付ける表式が得られる。
| ω=ω0-0.21kiso/P(T) | (13) |
この式は、温度一定の条件下で、ピーク位置ω は異性化反応速度kiso に比例して変化し、kiso =0の極限ではωは温度に拘わらず一定値ω0に収斂することを示しており、実験に得られたkisoとωの相関を見事に説明する。逆に図11の実験結果は、kisoとW1の間に(12)の関係が成立することを強く示唆している。図11と式(13)から、ω0 およびP(T)が表2のように求められる。
| T/K | W1/kiso | P(T)x10-3 | ΔE’/kcal mol-1 |
|---|---|---|---|
| 283 | 480 | 2.1 | 3.5 |
| 293 | 440 | 2.3 | 3.5 |
| 298 | 420 | 2.4 | 3.6 |
| 303 | 410 | 2.4 | 3.6 |
| 313 | 380 | 2.6 | 3.7 |
| ω0 =1577.4cm-1 | |||
ここで、W1/kisoは、動的分極の頻度の異性化速度に対する比であり、動的分極が何回起これば異性化が1回起こるかを表わす数である。
表1および2に得られたパラメーターを基にして、S1trans-スチルベンの異性化反応の微視的機構を、定量的にモデル化することができる(異性化反応の動的分極モデル、図13)。
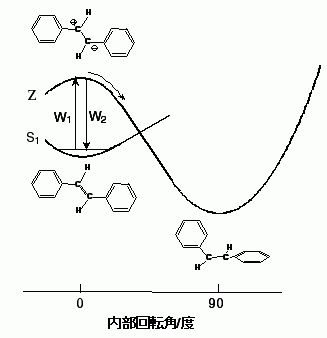
図13: S1trans-スチルベンの異性化反応の動的分極モデル。
ヘキサン、オクタン、デカンのアルカン溶媒中のS1trans-スチルベンは、常温付近で1ピコ秒に3から12回の割合で動的に分極する。もし分極が大きく、かつその分極状態が十分に長い時間持続すると、S1trans-スチルベンはz状態のポテンシャルに沿って、90°ねじれ型へと異性化する。400から500回(表2のW1/kiso)の動的分極に対して1回の割合でこのような条件を満たす分極が起こり、その結果異性化が進行する。このように考えると、ピコ秒時間分解ラマン分光によって得られたスペクトルデータを、全て満足に説明することができる。即ち、観測されたC=C2重結合バンド形の溶媒、温度依存性は、動的分極の頻度W1の溶媒、温度依存性に帰着され、同じW1によって決まる異性化反応速度の溶媒、温度依存性と定量的に関係付けられるのである。
動的分極モデルとArrheniusの式
化学反応論の基本式としてArrheniusの式が知られている。
| kiso=Aexp(-ΔE/RT) | (14) |
ここでAは頻度因子、ΔEは活性化エネルギー、Rはガス定数である。動的分極モデルによって異性化反応速度を表わす表式(12)は、Arrhenius式(14)と似た形をしている。この2つの式を比べると、頻度因子Aはs-1の次元を持つので、W1と対応すると考えられる。そうすると、無次元のエネルギー因子exp(-ΔE/RT)は、P(T)に対応することになる。そこで形式的にP(T)=
exp(-ΔE’/RT)と置いて-ΔE’を求めると、表2に示すように3.5から3.7 kcal mol-1の値が得られる。一方、粘度の等しい混合アルカン溶媒中、室温付近での蛍光寿命測定により求めたkisoの温度依存性から、ΔE
=3.5kcal mol-1が得られている[9]。即ち、(12)と(14)は形が似ているばかりでなく、それぞれの因子が定量的に良く一致する。別の言い方をすれば、ラマンバンドのピーク位置の解析から、Arrhenius式の頻度因子Aが求まったことになる。Arrhenius式を導く理論的アプローチはいくつか知られているが、動的分極理論はそれらと全く異なる観点から、Arrhenius式と同等と考えられる表式(12)を導出したことになる。
Arrhenius式は、従来の化学反応論で広く用いられて来た経験式である。この式は、巨視的な分子アンサンブルについての統計平均した反応速度を与えるものであり、反応の微視的機構については何も語らない。例えば、反応がどのようなきっかけで開始し、どのような時間スケールで進行するのか、また反応の途中で電子状態がどのように変化するのか、など反応の分子論的本質に関わることは、Arrhenius式からは全く窺がい知ることができない。一方、動的分極モデルは、溶液中のS1trans-スチルベンの異性化反応について、明確かつ定量的な描像を与える。即ちこのモデルでは、溶液中のS1trans-スチルベン分子は、溶媒の作る電場の揺動により1ピコ秒に数回の割合で分極し、中央の炭素-炭素結合がCΔ+-CΔ-のような電子状態をとる。その結果、炭素-炭素結合の回転が起こりやすくなり、分極数百回に対し1回の割合で異性化反応が進行する。1個の分子が反応する様子を、まるで見てきたかのように描写することができるのが、動的分極モデルの特徴である。
動的分極モデルの確立に向けて
化学反応の動的分極モデルをさらに検証するためには、超高速時間分解ラマン分光を用いて数多くの反応素過程を観測し、図11のような素反応速度と反応物のラマンバンド形の関係を定量的に調べて行くことが必要である。図3の装置では、プローブ波長が600nm近辺に、したがってポンプ波長が300nm近辺に限定されていた。そのため、S1trans-スチルベンの異性化以外の素反応に研究を拡張することが困難であった。現在、この困難を解消するために、より広い波長領域で実験が可能なTi:Sapphireレーザーシステムによるピコ秒時間分解ラマン分光装置を製作中である。また、赤外吸収バンド形についても動的分極モデルに基づくアプローチが可能であり、超高速時間分解赤外分光による同様の研究を開始したところである。
結語
筆者は、科学研究が陸上競技の3段とびのスキームで進歩すると考えている。まず新しい測定手法の開発により、測定の確度、精度、感度が不連続的に向上し、それまで不可能であった測定が可能となる(ホップ)。次に、開発された新しい測定法によって、それまで知られていなかった新しい現象が発見される(ステップ)。そして、発見された新しい現象が、新しい理論に基づいて解明され、最終的に新しい理念や法則として確立される(ジャンプ)。ここで示した研究例では、極限に近い高い感度と、フーリエ変換限界に迫る高い時間・エネルギー確度を持つピコ秒時間分解ラマン分光の開発により、それまで不可能であった短寿命中間体のラマンスペクトルを高いS/N比で測定し、バンド形の溶媒効果や温度依存性を高い精度で調べることが可能になった(ホップ)。続いて、S1trans-スチルベンのC=C2重結合バンドの形が溶媒や温度に依存して系統的に変化し、ピーク位置?が異性化反応速度kisoと特徴的な相関を持つという、従来の理論からは全く予見できない興味深い現象を見出した(ステップ)。そして最後に、溶媒誘起動的分極という新しい概念を導入することにより、これらの予想外の実験結果をすべて理論的に説明し、溶液中の化学反応の基本的モデルであるtrans-スチルベンの異性化反応の微視的機構について、分子論的視点からの洞察を深めることができた。この研究は依然継続中であって、筆者等が提唱する化学反応の動的分極モデルは未だ作業仮説の段階にある。3段とびのスキームでは、ステップからジャンプへの移行の過程にあると言える。現在、trans-スチルベンの異性化反応に加えて、プロトン移動反応などいくつかの化学反応素過程についても、動的分極モデルが適用できることを示唆する実験結果が得られている。それらの解明により、大きなジャンプ曲線を描いて未踏の地に着地することを目指して研究を続けている。
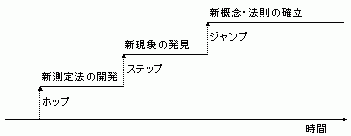
図14.科学研究の3段とび
研究3段とびのすべての段階での面白さを、個人レベルで味わうことができるのが物理化学研究の醍醐味である。筆者はそのうちでも特にホップの段階が最も好きである。ホップ、即ち新しい測定法の開発がなければ、真に新しいことは始まらないからである。
謝辞
本稿は、岩田耕一、小澤亮介の両氏との共同研究による成果を、その背景を含めて一般向けに解説したものである。両氏に感謝する。
文献
- K. Iwata, S. Yamaguchi and H. Hamaguchi, Rev. Sci. Instrum. 64, 2140 (1993).
- R. M. Hochstrasser, Pure and Appl. Chem.52, 2683 (1980).
- H. Hamaguchi and K. Iwata, Chem. Phys. Lett. 208, 465 (1993).
- V. Deckert, K. Iwata and H. Hamaguchi, J. Photochem and Photobiol. A, 102, 35 (1996).
- K. Iwata, R. Ozawa and H. Hamaguchi, J. Phys. Chem. 106, 3614 (2002).
- K. Iwata and H. Hamaguchi, J. Phys. Chem. A, 101, 632 (1997).
- H. Hamaguchi, Mol. Phys. 89, 463 (1996).
- D. Watanabe, Master Thesis, The University of Tokyo (2004).
- S. K. Kim, S. H. Courtney and G. R. Fleming, Chem. Phys. Lett. 169, 543 (1989).