
���}���U���̌ÓT�_�Ɨʎq�_
���}���U���̗��_�ɂ͏��w�҂ɂƂ��ē���ȕ���������A���}���������ԊO�����قǕ��y���Ȃ���̗v���ƂȂ��Ă���B�ȉ��ł́A���̃G�b�Z���X���ł�����蕽�Ղɉ�����邱�Ƃ����݂�B�܂��ÓT�_�ɂ��U�����}���U���̋@�\�𖾂炩�ɂ��A�U�����x��^����\���o����B����Ɋ�Â��āA�I�𗥁A�Ό������B���ɗʎq�_�ɂ����Kramers-Heisenberg-Dirac(KHD)���U���o���铹�������B������Placzek�̕��ɗ����_�ɂ���ČÓT�_�Ƃ̑Ή�����������AAlbrecht�̐U�d���_�ɂ�苤���}���U���̋��x��莮������B��茵���ȗ��_�ɂ��ẮA���ȏ�1)���Q�Ƃ��Ē��������B
�U�����}���U���̌ÓT�_
���˓d���g
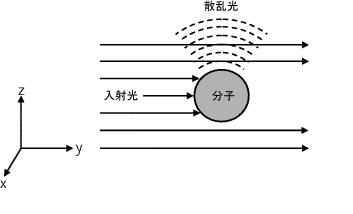
�U�����}���U���U���̌ÓT�_�ł́A���ˌ��ʓd���g�Ƃ��Ď�舵���A���q����U���ɂ���Ď����I�ɕϓ����镪�ɗ��������q�Ƃ��ă��f��������B�U�����́A��ԂɌŒ肳�ꂽ���q�ɗU�N���ꂽ�U�N�o�Ɏq�\������ˏo����鋅�ʓd���g�i2���g�j�Ƃ��ĕ\�킳���i�}1�j�B
�}1: �U�����}���U���̌ÓT�_�I��舵���i90���U���̏ꍇ���ɂƂ��Ă���j
���˕��ʓd���g�̓d��x�N�g��Ei�����̂悤�ɕ\�킷�B
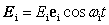 (1)
(1)������Ei�͓��ˌ��d��̐U���Aei�͕Ό��x�N�g���Aωi�͊p�U�����ł���B�x�N�g��ei��3�̐��������B
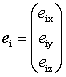 (2)
(2)�����ŁAx,y,z�͂��ꂼ���ԌŒ�̃f�J���g���W�ł���i�}1�j�B
���q�̕��ɗ�
���q�̕��ɗ�α��2�K�̑Ώ̃e���\���ŁA6�̓Ɨ��Ȑ��������B
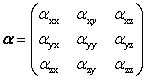 (3)
(3)�����ŁAαxy=αyx,αyz=αzy,αxz=αzx�̊W������B���ɗ�α�͕��q�̌��q�j�z�u�̊��ł���A����WQk�̊��Ƃ��ĕ\�킷���Ƃ��ł���B�����ŁAQk�͕��q��k�Ԗڂ̊���W�ł���B���ɗ��̐���αρσ��Qk�̙p�����Ƃ��ēW�J���A1���̍��܂Ŏc���Ǝ�����������B������ρ�����σ�́Ax�Ay�Az�̂����ꂩ���w�����̂Ƃ���B
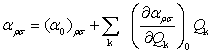 (4)
(4)�����ŁA(α0)ρσ�͌��q�j�̕��t�ʒu�ɂ����镪�ɗ��A(∂αρσ/∂Qk)0�͊j�̕��t�ʒu�ɂ����镪�ɗ�����αρσ��k�Ԗڂ̊���W�ɂ����W���ł���B���q�͊���W�ɉ����Ċp�U����ωk�Ŏ����I�ɉ^������B���̍ۂ̌��q�j�̈ʒu�͊���W�ɂ���Ď��̂悤�ɕ\�킳���B
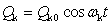 (5)
(5)��(5)��(4)�ɑ������ƁA���ɗ�����αρσ�̎��ԕω���\�킷����������B
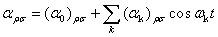 (6)
(6)�����ŁA(αk)ρσ�͎����I�ɕϓ����镔���̐U���ŁA�����ŗ^������B
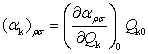 (7)
(7)�U�N�o�Ɏq�\��
���ˌ��̓d��ɂ���ĕ��q�ɗU�N�����o�Ɏq�\��μ��(1)��(6)�̐ςŗ^������B����μρ�ŏ����Ǝ��̂悤�ɂȂ�B
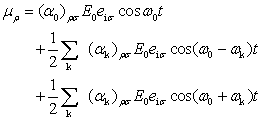 (8)
(8)�����A�U�N�o�Ɏq�\���ɂ́Aω0�Aω0-ωk�Aω0+ωk��3��̊p�U�����ŐU������3�̐������܂܂��B�����I�ɕϓ�����o�Ɏq�\���́A���̊p�U�����Ɠ����p�U�����̓d���g����˂���B���������āA��(8)�̗U�N�o�Ɏq�\������́Aω0�Aω0-ωk�Aω0+ωk��3��̊p�U�������������d���g�����˂����B�p�U����ω0�̐��������[���[�U���Aω0-ωk�̐������X�g�[�N�X-���}���U���Aω0+ωk�̐������A���`�X�g�[�N�X-���}���U���ł���B���̂悤�ɂ��āA���}���U������������@�\���ÓT�_�I�ɖ��炩�ƂȂ����B
���U���̋��x
���q�����_�ɒu���A�U�N�o�Ɏq�\��μ����ˏo����鋅�ʎU���g�̈ʒuR�ɂ�����d��x�N�g��Es���A�U��Es�ƕΌ��x�N�g��es�̐ςƂ��ĕ\�킷�i�}2�j�B
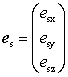 (9)
(9)������es�́AR�ɐ����ȕ��ʂւ�μ�̎ˉe�ƕ��s�ł���
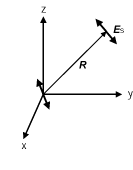
�}2: �U�N�o�Ɏq�\���ƈʒuR�ɂ�����U�����̓d��x�N�g��
Maxwell�������ɂ��AEs��μ�Ǝ��̂悤�ɊW�Â�����B
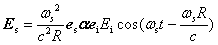 (10)
(10)�����ŁAωs�͎U�����̊p�U�����Ac�͌����x�AR��R�̐�Βl�ł���B��(10)�̗��ӂ�2�悷�邱�Ƃɂ��A���˕��ʓd���g�̋��xI0�i�P�ʎ��ԂɒP�ʖʐς�ʂ��ė������ˌ��G�l���M�[�j�ƁA�U�����ʓd���g�̋��xIsR2�i�P�ʎ��ԂɒP�ʗ��̊p��ʂ��ė����U�����G�l���M�[�j���W�Â�����B
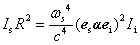 (11)
(11)���ꂪ�ÓT�_�ɂ���ċ��߂����U���̋��x��\�킷�\���ł���B�����ŁA���ɗ��e���\��α���A�U���e���\��a�Œu���������B���[���[�U���ł�a=α0�A���}���U���ł�a=αk/2�ł���B��(11)�́A���U���̋��x���A���ˌ��̋��xI0�ɔ�Ⴕ�A�U���e���\��a��2��A�U�����̊p�U����ωs��4��ɔ�Ⴗ��i������ν4���j���Ƃ������Ă���B
���}���U���̑I�𗥁A�X�g�[�N�X/�A���`�X�g�[�N�X���x��
���}���U���̑I�𗥂́A���ɗ��̐����̂ǂꂩ1��(αk)ρσ���A�[���łȂ��l�����Ƃ����������瓱�����B
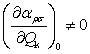 (12)
(12)�����Ak�Ԗڂ̊���WQi�ɑΉ������U�������}���U���Ɋ����ł��邽�߂ɂ́A���̊���W�ɂ����W�����[���łȂ����ɗ����������Ȃ��Ƃ�1���݂��Ȃ���Ȃ�Ȃ��B����������ƁA���q�j�̕��t�ʒu�ɂ����āA���ɗ�������ω�������悤�ȑΏ̐�������U�������}�������ƂȂ�B���o�̉ߒ����疾�炩�Ȃ悤�ɁA�X�g�[�N�X���}���U���ƃA���`�X�g�[�N�X���}���U���̑I�𗥂͓���ł���B�U�����ʊԂ̃{���c�}�����z�����肷��ƁA�X�g�[�N�X�U���ƃA���`�X�g�[�N�X�U���̋��x��Isanti-Stokes/IsStokes�͎��̂悤�ɗ^������B
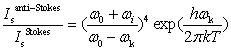 (13)
(13)������h�̓v�����N�萔�Ak�̓{���c�}���萔�AT�͐�Ή��x�ł���B��(13)��p����A�����̃��}���U�����x���玎���̉��x�����߂邱�Ƃ��ł���B���q�v���@��p���Č����x�����q���Ƃ��đ��肷������ł́Aωs��4��ɗR����������3��Ƃ��Ȃ���Ȃ�Ȃ��̂Œ��ӂ�v����B
���U���̕Ό������x
�}1��y�����ɐi�s���Ax�����ɕΌ��������ˌ����Az�����֎U�������ꍇ���l����i90���U���j�B�U�����ɂ�x�����ɕΌ����镽�s�����ƁAy�����ɕΌ����鐂���������܂܂��B���s�����̋��xI∥�͎�(11)��
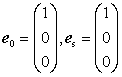
�������āA���̂悤�ɋ��߂���B
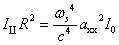 (14)
(14)���l�ɂ��Đ��������̋��xI⊥�͎��̂悤�Ɍv�Z�����B
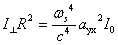 (15)
(15)���������̋��xI⊥�̕��s�����̋��xI∥�ɑ�����Ό������xρ�ƌĂԁB���l�@���Ă���悤�ɁA���q����ԂɌŒ肳��Ă���n�i�Ⴆ�ΒP���������j�ł́A�Ό������xρ�͎U���e���\�������̔�̂Q���^����B
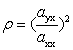 (16)
(16)�n�t�A�t�̂ȂǕ��q�̔z���������_���Ȍn�ł́Aρ�͎U���e���\����3�̉�]�s�ϗʁAG0�i�g���[�X�����j�AGs�i�Ώ̐����j�AGa�i���Ώ̐����j�ɂ�莟�̂悤�ɕ\�킳���B
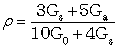 (17)
(17)�������A�ÓT�_�͈̔͂ł́A�U���e���\���͑Ώ̃e���\���ł���̂ŁAGa=0�ƂȂ�Aρ �̂Ƃ蓾��l��0��ρ��0.75�Ɍ�����B��ɏq�ׂ鋤���}���U���ł́A���}���U���e���\������Ώ̂ƂȂ�(Ga���O)�A�ُ�Ό������x�iρ>0.75�j���ϑ�����邱�Ƃ�����B2)
���}���U���̗ʎq�_
���}���U���̗ʎq�_�ł́A�p�U����ωi�A�Ό��׃N�g��ei�̓��ˌ��q��1���ł��A�p�U����ωs�A�Ό��׃N�g��es�̎U�����q��1��������Ɠ����ɁA���q���n���|m>����I���|n>�֑J�ڂ���ߒ��̊m�����v�Z����i�}3�j�B
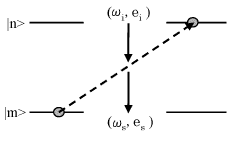
�}3: ���}���U���̉ߒ�
�d�����ʎq���������q�̌����|ni,ns>�Ō��̏�Ԃ�\�킷�B�����ŁAni�͊p�U����ωi�A�Ό��׃N�g��ei�������q�̌��Ans�͊p�U����ωs�A�Ό��׃N�g��es�������q�̌��ł���B���}���U���ߒ��̎n���|i>�ƏI���|f>�́A���̏�Ԃƕ��q�̏�Ԃ̐ςƂ��Ď��̂悤�ɕ\�킳���B
| |i>=|ni,ns>|m> | (18) | |
| |f>=|ni-1,ns+1>|n> | (19) |
���ƕ��q�̃n�~���g�j�A��
���Ƒ��ݍ�p���镪�q�n�̃n�~���g�j�A��H�́A���̃n�~���g�j�A��Hrad�A���q�̃n�~���g�j�A��Hmol�A���ƕ��q�̑��ݍ�p�n�~���g�j�A��Hint�̘a�Ƃ��ĕ\�킳���B
���̃n�~���g�j�A���́A���q�̌���Ԃ��ŗL��ԂƂ��Ď����A�ȉ��̌ŗL�����������B
| Hrad| ni,ns>=(niEi+nsEs) | ni,ns> | (20) |
�����ŁAEi=hωi/2π �����Es=hωs/2π��,���ꂼ����ˌ��q����юU�����q�̃G�l���M�[�ł���B
���q�̃n�~���g�j�A���́A���̌ŗL�����������B
| Hmol|m>= Em|m> | (21) | |
| Hmol|n>= En|n> | (22) | |
| Hmol|e>= Ee|e> | (23) |
�����ŁA���q�̎n���|m>�ƏI���|n>�ɉ����āA���ԏ��|e>���l�����Ă���B��ɏq�ׂ�悤��|e>�͒P��̏�Ԃł͂Ȃ��A�����̒��ԏ�Ԃ̏W����\�킷���̂ƍl����BEm�AEn�AEe�͂��ꂼ��|m>�A|n>�A|e>�̃G�l���M�[�ł���B
�ƕ��q�̑��ݍ�p�n�~���g�j�A���́A�ÓT�_�I�ɂ͕��q�̑o�Ɏq�\��D�ƌ��d��E�̐ςƂ��ĕ\�킳���B����ɑΉ�����ʎq���������ݍ�p�n�~���g�j�A���́A���̂悤�Ȍ`�����Ă���B
| Hint�`Dei(âi+â†i)+ Des(âs+â†s) | (24) |
������âi�Aâ†i�����âs�Aâ†s�͂��ꂼ����ˌ��q����юU�����q�̏��ŁA�����̉��Z�q�ŁA�Ⴆ�Γ��ˌ��q�̌����ȉ��̎��ɏ]���ĕω�������B
| âi| ni,ns>=(ni)1/2 | ni-1,ns> | (25) | |
| â†i| ni,ns>=(ni+1)1/2 | ni+1,ns> | (26) |
���}���U���̒��ԏ��
��(24)�̑��ݍ�p�n�~���g�j�A���́A���q�̌���1�����ω������邱�Ƃ��ł���B2�̌��q���W���郉�}���U���́A���̑��ݍ�p�n�~���g�j�A����2��g����2���̐ۓ����瓱�����B���}���U���̎n���(18)�ƏI���(19)���������钆�ԏ�Ԃɂ́A2�̎�ނ�����B��1�̒��ԏ��|v1>�́A���ˌ��q��1�z�����ꂽ���̏��|ni-1,ns>�ƕ��q�̒��ԏ��|e>�̐ςŕ\�킳��A��2�̒��ԏ��|v2>�́A�U�����q��1���o���ꂽ���̏��|ni,ns+1>��|e>�̐ςŕ\�킳���B
| |v1>=|ni-1,ns>|e> | (27) | |
| |v2>=|ni,ns+1>|e> | (28) |
��ɎU�����q�����o����钆�ԏ��|v2>�̑��݂͈ꌩ�s�v�c�Ɏv���邪�A���q�̒��ԏ�Ԃ��n��Ԃ��������ȃG�l���M�[�����ꍇ�����邱�Ƃɒ��ӂ���A�}4�̃_�C�A�O�����Ŕ[�����邱�Ƃ��ł���B2��ނ̒��ԏ�Ԃ̑��݂́A���}���U�����i�z���ƕ��o��2��1���q�ߒ�����Ȃ�j�u���Ƃ͖��Ăɋ�ʂ����2���q�ߒ��ł��邱�Ƃ������Ă���B
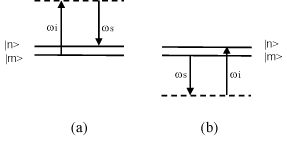
�}4: ���}���U���Ɋ܂܂��2��ނ̉ߒ�; a) ���ˌ��q��1�z�����ꂽ���ԏ�Ԃ��o�R����ߒ� b) �U�����q��1���o���ꂽ���ԏ�Ԃ��o�R����ߒ�. �j���͉��z�I�Ȓ��ԏ�ԁi��o�j������
Kramers-Heisenberg-Dirac�̕��U��
����ʎq�_�ň����ꍇ�A���̋��x�Ƃ��ĒP�ʎ��ԂɒP�ʖʐς�ʂ��ė������q���A���Ȃ킿���q�t���b�N�XF��p����̂��֗��ł���B���q�t���b�N�X�ƑΉ�����d���g�̋��xI�́A���̂悤�ɊW�t������B
| I=hωF/2π | (29) |
������hω/2π�͌��q�̃G�l���M�[�ł���B
��(18)����(29)��p���A2���̐ۓ��_��p���ă��}���U���̋N����m�����v�Z����ƁA�ȉ��̎���������B�������A(18)��(19)��ns=0�Ƃ����A�������}���U���݂̂��l�����B
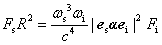 |
(30) | |
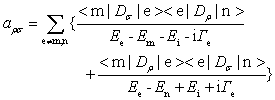 |
(31) |
��(30)�͓��ˌ��q�t���b�N�X�ƎU�����q�t���b�N�X�����т��鎮�ł���A�ÓT�_�̎�(11)�ɑΉ�����ʎq�_�̕\���ł���B��(31)�����q�̗ʎq��Ԃɂ���ĕ\�킳�ꂽ���}���U���e���\�������̕\���ŁA�ŏ�Kramers��Heisenberg3)�ɂ���Ĕ��ÓT�_�I�ɓ��o����A���Dirac4)�ɂ���ėʎq�_�I�ɓ��o���ꂽKramers-Heisenberg-Dirac�iKHD�j�̕��U���ł���B
KHD�̕��U���̕����I�Ӗ�
KHD�̕��U��(31)�́A���q�̎n���|m>�A�I���|n>�ȊO�̂����钆�ԏ��|e>�Ɋւ��鋁�a���܂�ł���B���ꂼ��̒��ԏ�Ԃ̊�^���ʑ��������� (��Βl��2�� | |2���Ƃ�O��) ���a����邱�Ƃ́A���}���U���̉ߒ��ŕ��q�����ԏ��|e>�Ɏ��ۂɕ��z����킯�ł͂Ȃ����Ƃ������Ă���B���̈Ӗ��Œ��ԏ�Ԃ͉��z�I�ivirtual�j�ł���ƌ�����B�e���ԏ�Ԃ̓G�l���M�[����ɋt��Ⴕ�ĎU���e���\�������Ɋ�^����B�G�l���M�[����́A���q�G�l���M�[���܂߂����ԏ�ԂƎn��Ԃ̃G�l���M�[���ƁA���������ɂ����锭�U������邽�߂Ɍ��ۘ_�I�ɓ������ꂽ�ɘa��iΓe�̘a�̌`�ɂȂ��Ă���B
��(31)��{ }���̑�1���́A��(27)�̒��ԏ�ԁi�}4(a)�j�ɑΉ����A�܂�σ�����ɕΌ��������ˌ��q�����ݍ�p<m|Dσ|e>�ɂ����1���ł��A������ρ�����ɕΌ������U�����q��<e|Dρ|n>�ɂ����1��������ߒ���\�킵�Ă���B�G�l���M�[����́A���ԏ�ԂƎn��Ԃ̃G�l���M�[��Ee-Em-Ei�Ɗɘa��iΓe����Ȃ�B��2���́A��(28)�̒��ԏ�ԁi�}4(b)�j�ɑΉ����Aρ�����ɕΌ������U�����q��<m|Dρ|e>�ɂ����1�������A������σ�����ɕΌ������U�����q��<e|Dσ|n>�ɂ����1��������ߒ���\�킵�Ă���B�G�l���M�[����́A���ԏ�ԂƎn��Ԃ̃G�l���M�[��Ee-Em+Es=Ee-En�{Ei�Ɗɘa��iΓe����Ȃ�B�����ŁA�G�l���M�[�ۑ��̎�Em+Ei=En+Es��p�����B�܂��A�ŋ߂�Buckingham��Fischer5)�̒�Ăɏ]���A�_���s���O���̕������1���ł̓}�C�i�X�ɁA��2���ł̓v���X�ɂƂ��Ă���B
���d�q��Ԃ̐U�����}���U���Ɠd�q������
KHD�̕��U�����A��X���ł������������d�q��Ԃ̐U�����}���U���ɓK�p����B���̂��߂ɁA���q�̎n��ԁA�I��ԁA���ԏ�Ԃ�d�q��ԂƐU����Ԃ̐ςƂ��ĕ\�킷�i�f�M�ߎ��j�B
| |m>=|g]|i) | (32) | |
| |n>=|g]|f) | (33) | |
| |e>=|e]|v) | (34) |
������| ]�����| )�́A���ꂼ��d�q��ԂƐU����Ԃ�\�킷��ԃx�N�g���ŁA|g]�͊��d�q��ԁA|e]�͗�N�d�q��Ԃ��A|i)�A |f)�A |v)�͂��ꂼ��U���̎n�A�I�A���ԏ�Ԃ������i�}5(a)�j�B�ώG��������邽�߂ɁA���d�q��Ԃ͏k�d���Ă��Ȃ����̂Ƃ���B
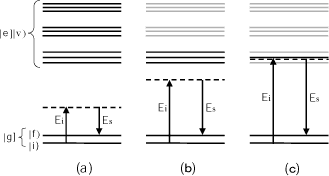
�}5: ���d�q��Ԃ̐U�����}���U���̐U�����}���U���̃_�C�A�O����; (a)�A(b)�O�����A(c)�^�����B���ԏ�ԂƂ��Ă̊�^���傫��|e]|v)��Z�������Ŏ����Ă���B
���d�q���|g]�̐U�����}���U���ł́A���ԓd�q���|e]��|g]���傫�ȃG�l���M�[�������A�}4(a)�̉ߒ�����v�Ȋ�^�������B���ԏ��|e]|v)�Ǝn���|g]|i)�Ƃ̃G�l���M�[��Eev-Egi�ƁA��N���̃G�l���M�[Ei�̑��ΓI�ȑ傫���ɂ���āA��N������A�O�����A�^������3�̃J�e�S���[�ɕ��ނ���i�}5�j�B�ł́AEev-Egi�� Ei�ɔ�ׂĈ��|�I�ɑ傫���A�G�l���M�[�����Eev-Egi-Ei�̍��́A�����̒��ԏ�Ԃɑ��ē����x�̑傫���ƂȂ�B���̌��ʁA������|e]|v)�����ׂĒ��ԏ�ԂƂ��Ċ�^����i�}5(a)�j�B�O�����ł́AEi��Eev-Egi�ɋ߂Â��A�G�l���M�[���ł��Ⴂ���ԓd�q��Ԃɑ�����U�d��Ԃ��傫�Ȋ�^�����i�}5(b)�j�B�^�����ł́AEi��Eev-Egi�ɂقړ������Ȃ�A����̐U�d��Ԃ݂̂����}���U���Ɋ�^����i�}5(c)�j�B��(32)����(34)��(31)�ɑ������ƁA�f�M�ߎ��̉��ł̊��d�q��Ԃɂ�����U�����}���U���e���\���̕\����������B
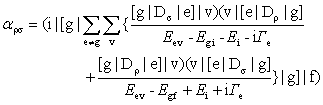 (35)
(35)�U�����}���U�� (Placzek�̕��ɗ����_)
�������ł�Eev-Egi>>Ei> �ł���AEev-Egi-Ei���U���G�l���M�[�ɔ�ׂď\���ɑ傫���̂ŁAEev-Egi-Ei~Ee-Eg-Ei���ǂ��ߎ��Ő�������B�����ŁAEe��Eg�͂��ꂼ��|e]��|g]�̓d�q�G�l���M�[�ł���B�܂�Eev-Egi-Ei��iΓe�ɔ�ׂĂ��\���ɑ傫���̂ŁAiΓe������B��������ƁA��(35)��v�ɂ��Ă̋��a�͇�|v><v|�ƂȂ�A�����|v>�̊��S������1�ɓ������B���ʂƂ��Ē��ԓd�q���|e]�ɑ�����U������|v>�̊�^���ۂߍ��܂�A��(35)�͎��̂悤�ɂȂ�B
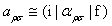 (36)
(36)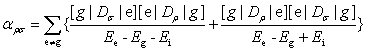 (37)
(37)������(37)�́A���q�̕��ɗ��̗ʎq�_�I�\���ł���B��(36)�́A�������ŁA�U�����}���U���e���\������aρσ���A���ɗ��e���\������αρσ�̐U���s��v�f(i|αρσ|f)�ɂ���ċߎ��I�ɗ^�����邱�Ƃ������Ă���(Placzek�̕��ɗ����_)�B
�U�����|i)�����|f)�́A�ǂ��ߎ��Œ��a�U���q�̌ŗL��Ԃ̐�π|vki)�����π|vkf)�ŕ\�킳���B�����ŁAvki�����vkf�́A�n��ԂƏI��Ԃɂ�����k�Ԗڂ̐U�����[�h�̗ʎq���ł���B���a�U���q�̌ŗL��Ԃ̐�������A���̊W��������B
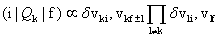 (39)
(39)��(37)�ŗ^�����镪�ɗ��́A����WQi�̊��ł���̂ŁA�ÓT�_�̏ꍇ�Ɠ��l�ɁA��(4)�̂悤��Qi�̙p�����ɓW�J���邱�Ƃ��ł���B���̓W�J����(39)�̊W����A���ɗ����_�̘g�g�݂̒��ł̐U�����}���U���̑I�𗥂�������B
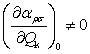 (12)
(12)| Δv=vkf-vki=�}1 | (40) |
���ɗ������̑Ώ̐��Ɋւ���I��(12)�́A�ÓT�_�I�ɓ��o���ꂽ���̂Ɠ���ł���A�ʎq�_�ł͂���ɐU���ʎq���Ɋւ���I��(40)���t�������B��(40)�̉E�ӂ́{�����̓X�g�[�N�X�U���A-�����̓A���`-�X�g�[�N�X�U���ɑΉ�����B�ʏ�ϑ������U������Ԃ���̃X�g�[�N�X���}���U���ł́Avki=0�Avkf =1�ł���B
���U�����}���U���iAlbrecht�̐U�d���_�j
�O������^�����̏������ł́A���ԏ�Ԃ̐U�d�I������I�ɍl������K�v������B���̂��߂ɁA���q�̃n�~���g�j�A��Hmol��d�q���W�݂̂��܂�Hmole�A���q�j���W�݂̂��܂�Hmolv ����ѓd�q�ƌ��q�j�̍��W���Ɋ܂�Hmolev�ɕ������ĕ\�킷�B
| Hmol=Hmole+ Hmolv +Hmolev | (41) |
�����ŁAHmole���[�����̓d�q�n�~���g�j�A���AHmolv ���[�����̐U���n�~���g�j�A���Ƃ��AHmolev��1���̐ۓ��Ƃ��Ď�舵���B�[�����̓d�q�ŗL��ԂƂ��Ċ��d�q���|g0]�Ɨ�N�d�q���|e0]�����|s0]���l����B�����͂��ꂼ��G�l���M�[Eg0�A Ee0�AEs0�������A���̌ŗL�����������B
| Hmole|g0]= Eg0|g0] | (42) | |
| Hmole|e0]= Ee0|e0] | (43) | |
| Hmole|s0]= Es0|s0] | (44) |
�܂��A�U���̎n���|i)�A���ԏ��|v)�A�I���|f)�́A���ꂼ��Ei0�AEv0�AEf0�̃G�l���M�[�������A���̌ŗL�����������B
| Hmolv|i)= Ei0|i) | (45) | |
| Hmolv|v)= Ev0|v) | (46) | |
| Hmolv|f)= Ef0|f) | (47) |
��(41)��Hmolev��ۓ��Ƃ��Ĉ����ƁA|s0]�Ƃ̐U�d�q���ݍ�p�̌��ʂ�1���܂ōl���������ԓd�q���|e]�̕\����������iHerzberg-Teller�W�J�j�B
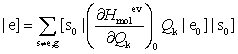 (48)
(48)�n����яI�d�q��ԂƂ���|g0]�A���ԓd�q��ԂƂ���|e]���Ƃ�A��(35)�ɑ������ƁA�f�M�ߎ��ŐU�d���ݍ�p��1���܂Ŏ����ꂽ����Ԃ̐U�����}���U���e���\�������܂�B�������A���ɂ���đ��傷��(35)�̑�1���i�����j�݂̂��l�������B
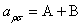 (49)
(49)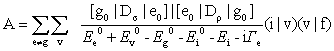 (50)
(50) (51)
(51)��(50)�����(51)�́A���ꂼ��Albrecht��A���iFranck-Condon���j�����B���i�U�d���ݍ�p���j�ƌĂ��B6)
A���ɂ́A���d�q���g����1���q���e�ȗ�N�d�q���e�݂̂��֗^���� (�}6 (a))�B���}���U�����x��Franck-Condon���q(i|v)(v|f)�ɂ���Č��܂�B���d�q���g�Ɨ�N�d�q���e�̕��t���q�j�z�u�̂���Δ���傫���Ȃ�ƁA(i|v)�����(v|f)�����܂��܂ȑg�ݍ��킹�ɑ��đ傫�Ȓl�������Ƃ��ł��AA���R���̋����}���U���������ϑ������B�d�q��N�ɂ���ĕ��q�̑Ώ̂��傫���ቺ�����O�I�ȏꍇ�������āA�傫��Δ�������Ƃ��ł���U���́A�S�Ώ̐U���i���q�̑Ώ̂�ቺ�����Ȃ��U���j�Ɍ�����B���������āAA���R���̋����}���U���ł́A�S�Ώ̐U���Ƃ��̍����{���iΔv>>1�j�̃o���h�������ϑ�����邱�Ƃ������B
B���ɂ́A�݂��ɐU�d���ݍ�p���Ă��āA���Ƃ���g����1���q���e��2�̗�N�d�q���e��s���֗^���� (�}6 (b))�B��N���̌��q�G�l���M�[��g����e�ւ̑J�ڃG�l���M�[�ɋ߂Â��ƁA�U�d���ݍ�p�ɂ��e��s�����������Ă���U�� (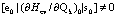 �����U��) �̃o���h�̋��x�����傷��BB���R���̋����}���U���ł́AΔ��0�̔�S�Ώ̐U���������ƂȂ�B�܂����i51�j�̐U���s��v�f�A(i|Qk|v)(v|f)�����(i|v)(v|Qk|f)����킩��悤�ɁA�����̔{���͏o�������AΔv��1�̑I�𗥂���������B
�����U��) �̃o���h�̋��x�����傷��BB���R���̋����}���U���ł́AΔ��0�̔�S�Ώ̐U���������ƂȂ�B�܂����i51�j�̐U���s��v�f�A(i|Qk|v)(v|f)�����(i|v)(v|Qk|f)����킩��悤�ɁA�����̔{���͏o�������AΔv��1�̑I�𗥂���������B
�ȏ�̂悤�ɁA�����}���U���ł́A�̏ꍇ�ƈقȂ�I�𗥂���������B�܂��A�k�d�������d�q��Ԃ�A���R���̋����}���U����AB���R���̋����}���U���ł́A���}���U���e���\������Ώ̂ƂȂ�A�Ό������x�ُ̈킪�����邱�Ƃ�����B
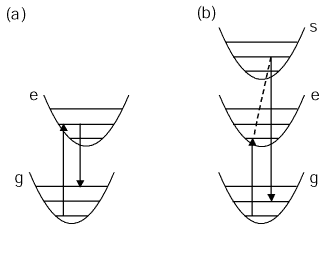
�}6: �U�������}���U���̑f�ߒ�; (a) A���ivki=0,vkv=1,vkf=2, (b) B�� (vki=0,vkv=0,vkf=1�j�B�j���͐U�d���ݍ�p��\�킷�B
�Q�l����
- 濵���G�v�A����Ŏq�ҁA���}�������@�A�w��o�ŃZ���^�[�A1988.
- H. Hamaguchi, Advances in Infrared and Raman Spectroscopy, R. J. H. Clark and R. E. Hester Eds., Wiley, Vol. 12, Capter 6.
- H. A. Kramers and W. Heisenberg, Z. Phys. 31, 681 (1925).
- P. A. M. Dirac, Proc. Roy. Soc. (London), A114, 710 (1927).
- A. D. Buckingham and P. Fischer, Phys. Rev. 61(3),5801(2000).