
分子のフェムト秒動的分極と化学反応
化学反応を理解するために様々な分極構造を持った中間体の存在が仮定されている。このような分極構造は本質的に動的なものである。超高速時間分解ラマン分光の助けを借り、反応直前の分子の振動位相緩和を観察することにより、反応の鍵を握る分子の動的分極構造を実体として捉えようと試みる。
プロローグ
筆者は過去10数年にわたって、新しい時間分解振動(ラマン・赤外)分光法の開発と,それを用いた溶液中の電子励起分子の構造とダイナミクスの解明,さらには電子励起に伴う高い反応性の本質を探る研究に携わってきた1)。その過程で,溶液中の電子励起分子のラマンバンド幅が,基底状態の分子のそれに比べて異常に広い場合が多々あることに気がついた。励起三重項状態で分子間電子移動錯体を形成するクロラニル,励起一重項及び三重項状態で分子内電子移動をおこすN,Nジメチルアミノベンゾニトリルなど,分極した構造を持つ励起分子で特にこの傾向が顕著であった。励起一重項状態のトランス-スチルベン(以下S1tSB)もその一つであった。
電子励起分子のラマンバンドはなぜ幅広い?
分子が振動しながら光の電場と相互作用しているとしよう。もし分子振動の位相と光電場の位相が一定の関係を保ったまま無限の時間相互作用したとすると、分子振動数とわずかでも違う振動数を持つ光電場との相互作用は時間的に平均するとゼロになってしまう。結果として得られる振動ラマンバンドの幅はゼロになるはずである。しかし現実にはこのような無限に鋭いスペクトルは観測されない。現実の系では振動の位相が乱されずにいる時間(位相緩和時間)が有限であり、分子と光の相互作用の時間が有限になるからである。振動位相緩和時間が短くなればなるほど振動バンドの幅は広くなる。分極した電子励起分子の異常に幅広いラマンバンドは,その位相緩和時間が基底状態の分子に比べて極めて短くなっていることの表れであると考えられる。
動的分極と振動位相緩和,ラマンバンド形
分極した電子励起分子に特徴的な振動位相緩和の機構を考察するために,筆者は以下に述べる動的分極モデルを導入した2)。溶液中の仮想的二原子分子C=Cを考えよう。溶媒との相互作用によって,C=C結合は分極する。この分極構造は,溶媒の揺動のために時間に依存して変化する。これを動的分極と呼ぶ。動的分極の結果,炭素-炭素伸縮角運動数ωは,C=C二重結合の角振動数ω1と、C+-C-単結合の角振動数ω2の間で確率論的に変動する(図1-c)。このときどのような振動バンド形が観測されるのだろうか。
この問題を解くために,動的分極モデルを単純化した2値問題(図1-a)から出発する。式で表すと(1)のようになる。ここでW1はω1からω2への平均の遷移速度(分極を誘起する揺動の頻度に対応する),W2はω2からω1への平均の遷移速度(1/W2はω2に留まる平均の時間)を表す。
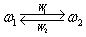 (1)
(1)
炭素-炭素結合がほとんど2重結合状態にあり(W1<<W2),動的分極の効果が小さい場合には,(1)のダイナミクスのもとでのラマンバンド形は,ピークがω1からΔωだけシフトし,幅がΔΓだけ広がったローレンツ形となる。
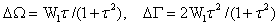 (2)
(2)
ただしτ=(ω2-ω1/W2である。バンド形は2つのパラメータW1とτで表されることがわかる。W1は前述のように動的分極が起こる頻度,τは平均の位相シフトで,一度の動的分極の大きさの平均値に対応した量である。
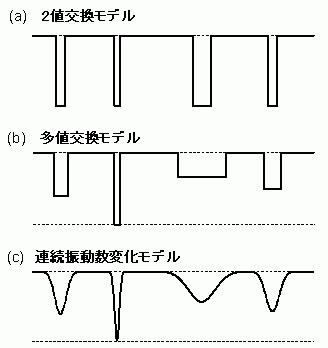
図1: 動的分極モデル
筆者は最近,図1-cのような一般の動的分極のもとでも,平均の位相シフトτが小さく,かつ位相シフトの分布関数がガウス関数で近似できる場合には,(2)と類似の関係が成立することを示した2)。
S1tSBの動的分極とラマンバンド形
tSB分子を溶液中で光励起すると,トランス型のS1状態がまず生成し,それが溶媒に強く依存した時定数(30-100ピコ秒)でねじれ型へ異性化する。S1tSBは反応直前の活性分子の優れたモデルである。
筆者等は,2.2ピコ秒の時間分解能と3.5cm-1の波数分解能を併せ持つ"フーリエ変換限界ピコ秒時間分解ラマン分光計を製作し3),溶液中のS1tSBのラマンスペクトルを詳細に調べた。その結果,中央jのC=C2重結合のラマンバンド形が溶媒に依存して明瞭な変化を示すことを見出した4)。どの溶媒中でもバンド形はローレンツ関数でよく表され,一連のアルカン溶媒中では,ピーク位置のシフトΔωとバンド幅の変化ΔΓの比が一定に保たれ,Δω/ΔΓ=-1.3の関係が成立することがわかった。
式(2)からΔω/ΔΓ=1/τの関係が得られる。実験式Δω/ΔΓ=-1.3はしたがって、,τ=-0.4がアルカン溶媒中で成立することを意味している。そうすると(2)より溶媒によるバンド形変化はW1のみによって決まる。実際,ヘキサンとドデカン中のC=C伸縮バンド形をW1のみをパラメーターとして極めて良く再現することができた。(図2)。このバンド形解析によって,ヘキサン中では370フェムト秒,ドデカン中では670フェムト秒に一回の割合で動的分極が起きていて,一回の動的分極の平均の時間は10フェムト秒であるというS1tSBのアルカン溶媒中の動的分極と振動位相緩和の描像が得られた。
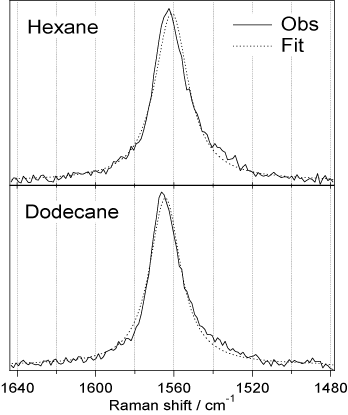
図2: 2値交換モデルによるS1trans-スチルベンC=C伸縮ラマンバンドのフィッティング
S1tSBの動的分極と異性化反応
S1tSBの異性化反応速度kisoは顕著な溶媒効果を示す。一連のアルカン溶媒に対して観測されたΔΓをkisoに対してプロットすると,綺麗な直線となり,ΔΓ=2.6×10-10kisoの関係が得られた。式(2)と,τ=-0.4を用いてΔΓをW1に置き換えると,W1=1.8×102kisoとなり,異性化反応速度が動的分極の頻度に比例することを示す関係が得られた。
この関係を図3の異性化反応のモデルで説明する。S1tSBは,C=C結合が分極した対イオン状態(図中のZ状態)の性格を,10フェムト秒程度の極短時間ではあるが持つことができる。Z状態が炭素-炭素結合が90°ねじれた安定構造を持つとすると,Zポテンシャル曲面上での時間発展速度W3を用いてkiso=W1W3/(W2+W3)と表すことができる。W2とW3がともに溶媒に依存しないと仮定すると,kisoはW1に比例した溶媒依存性を示すことになる。
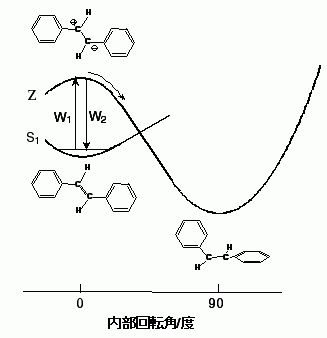
図3: Trans-スチルベンの光異性化反応の反応経路。
W1=1.8×102kisoの関係式は,動的分極180回に対して一回の割合で異性化反応が起こることを意味する。同じ式(kiso=5.6×10-3W1)をアレニウス式の形に書くとkiso=W1exp(-ΔE/kT),ΔE=3.1 kcal mol-1となり,独立に求まっていたΔE=3.5 kcal mol-1とよく対応した活性化エネルギーが得られた。動的分極を誘起する揺動のうちΔEよりおおきなエネルギーを持つもののみが異性化反応に寄与すると考えると,kisoとW1の関係をアレニウス式に準じて解釈することができる。
まとめ
フェムト秒動的分極の概念を導入することにより,溶液中のS1tSBの振動位相緩和(ラマンバンド形)と異性化反応速度の溶媒依存性を,同時かつ定量的に説明することができた。しかもアレニウス式に対応する関係式が自動的に導かれた。このことから,溶液中の化学反応の本質を捉えるうえで,動的分極モデルがそう的外れではないのだろうと筆者は考える。最後に,共同研究者である岩田耕一博士(神奈川科学技術アカデミー)に感謝する。
参考文献
- H. Hamaguchi and T. L. Gustgafson, Ann. Rev. Phys. Chem., 45, 593 (1994).
- H. Hamaguchi, Mol. Phys., in press.
- K. Iwata, S. Yamaguchi, and H. Hamaguchi, Rev, Sci, Instru., 64, 2140 (1993).
- H. Hamaguchi and K. Iwata, and H. Hamaguchi, J. Photochem. Photobiol. A, in press.