RECENT DEVELOPMENTS IN ULTRAFAST TIME-RESOLVED VIBRATIONAL SPECTROSCOPY OF ELECTRONICALLY EXCITED STATES
Abstract
Developments of three new time-resolved vibrational spectroscopies and their applications to electronically excited states are reviewed. Transform-limited picosecond time-resolved Raman spectroscopy has been used to study the vibrational dynamics of trans-stilbene in the lowest excited singlet state. Picosecond time-frequency two-dimensional multiplex CARS spectroscopy has been used to probe the structure of diphenylacetylene in the lowest and the second lowest excited singlet states. Nanosecond time-resolved dispersive infrared spectroscopy has detected the singlet and triplet intramolecular CT states of 4-(dimethylamino)benzonitrile. Strong evidence for a CT structure has been obtained.
1. Introduction
Structure and dynamics of electronically excited states has always been a matter of great concern in Chemical Physics. Luminescence spectroscopy, as developed by Professor Jablonski and other pioneers, is obviously one of the most powerful means for studying excited states. However, there are many kinds of interesting excited states that do not emit luminescence. Furthermore, the structural information obtained from luminescence spectroscopy is rather limited. These difficulties can be well compensated for by time-resolved vibrational (infrared and Raman) spectroscopy which looks directly into the structure of excited states [1,2].
In the present article, I briefly review our recent efforts for developing three new time-resolved vibrational spectroscopies and their applications to three electronically excited states of key importance. The new time-resolved vibrational spectroscopies include transform-limited picosecond time-resolved Raman spectroscopy, picosecond time-frequency two-dimensional multiplex CARS spectroscopy, and nanosecond time-resolved dispersive infrared spectroscopy. Though picosecond time-resolved Raman spectroscopy is very powerful in itself, it is not applicable to highly fluorescent excited states. For fluorescent excited states, picosecond CARS spectroscopy will be the choice. Time-resolved infrared spectroscopy is also important; vibrational information obtained by infrared spectroscopy is quite different from that obtained by Raman spectroscopy. The three time-resolved vibrational spectroscopies are thus complementary with one another.
Only brief overviews are given in this article. The readers are recommended to refer to the original papers for details.
2. Picosecond Time-resolved Raman spectroscopy
A transform-limited picosecond time-resolved Raman spectrometer was constructed based on an amplified dye laser system [3]. Time resolution of 2.2 ps and wavenumber resolution of 3.2 cm-1 have been achieved. The system was used to study the vibrational dynamics of S1 trans-stilbene (tSB) in solution. The significance of S1 tSB in the photophysical and photochemical studies of excited states is well known and is not repeated here.
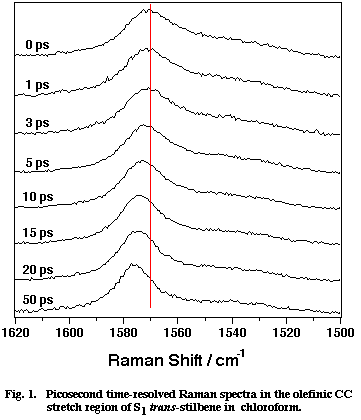
Fig. 1
Figure 1 shows a set of picosecond time-resolved Raman spectra of S1 tSB in chloroform (CHCl3) in the time range 0-50 ps after the photoexcitation. Marked spectral changes are observed for the olefinic CC stretch band at ∼1570 cm-1. In the first 20 ps, the peak position shifts to higher frequency and the band width decreases with increasing delay time. After 50 ps from the photoexcitation, the spectra remain the same. These spectral changes have been attributed to the vibrational cooling-down processes of the photogenerated S1 tSB. Note that S1 tSB carries an excess vibrational energy of about 2800 cm-1 with the photoexcitation. This conclusion has been drawn from the following two observations. First, the shift of the peak position and the decrease of the band width show exactly the same time dependence as that of the Stokes/anti-Stokes intensity ratio of the 280 cm-1 band, which is an indicator of the temperature of the S1 tSB molecule [4]. Second, the peak position and the band width at 50 ps delay (after the transient cooling down is over) were measured while varying the temperature of solution. The results show that the peak position and the band width linearly depend upon temperature [5,6]; in other words, the 1570 cm-1 band of S1 tSB can be regarded as a temperature indicator.
Using this picosecond Raman thermometer, we investigated the vibrational cooling-down kinetics of S1 tSB in ten different solvents. A strong correlation has been found between the observed cooling-down rate and the thermal diffusivity of the solvent [4]. In order to understand this correlation, we model the cooling-down process of the S1 tSB system in two steps; first the excess energy is distributed very rapidly (within much less than a few picosecond) among the solute S1 tSB and the solvents in the first coordination sphere, and then it is dissipated to the bulk solvent molecules following the ordinary heat conduction scheme (Figure 2). Picosecond Raman spectroscopy is thought to look at the second step whose rate is determined by the thermal diffusivity of the solvent. The observed correlation between the cooling-down rate and the solvent thermal diffusivity is thus qualitatively explained by the model in Figure 2.
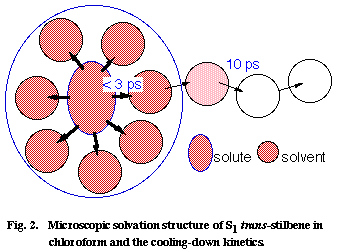
Fig. 2
Using a diffusion equation of heat, we can even quantitatively reproduce the cooling-down kinetics of S1 tSB in CHCl3, with an assumption that the excess energy is initially distributed homogeneously in a box with a 3.8 nm × 3.2 nm × 2.7 nm dimension (corresponding to S1 tSB with a 1.3 nm x 0.7 nm x 0.2 nm dimension plus the solvents in the first coordination sphere with a thickness of 1.25 nm) . We can finally estimate the number of CHCl3 molecules in the first coordination sphere from the observed temperature rise at 0 ps and the heat capacity of CHCl3 [6]. The number is 5 if V-T, V-R, and V-V processes are taken into account and is 12 if only V-T and V-R processes are considered. As far as the author knows, this is the first time that such microscopic details of the solute/solvent interaction is illuminated.
The reason why the position and the width of the olefinic CC stretch Raman Band change with time (temperature) has also been quested. There are a few clues for solving this problem [7]. First, the CC band shape is always a Lorentzian, suggesting that homogeneously broadening is the primary factor determining the band shape. Second, a clear linear relationship holds between the shift of the peak position (ΔΩ) and the change of the band width (ΔΓ) in the time (temperature) dependent changes. Third, a similar linear relationship between ΔΩ and ΔΓ holds for solvent dependent changes as well; spectra at 50 ps delay time were measured for seven different alkanes and solvent dependent ΔΩ and ΔΓ values were determined [7]. These facts indicate that the spectral change is not attributable to the simple hot band mechanism. Note that the contribution of hot transitions may cause temperature dependent band shape changes but it never accounts for the solvent dependent changes. It does not explain the observed ΔΩ/ΔΓ linear relationship, either. Alternatively, we introduce what we call the "dynamic polarization" model [7-9].
Suppose that the olefinic CC bond of S1 tSB is occasionally polarized into partial single bond Cδ+-Cδ- by the fluctuating solvent field or, in a more perceptible picture, by occasional collisions with the solvent (Figure 3). Then, following this dynamic polarization, the CC stretch frequency is stochastically modulated and the position and the width of the CC Raman band change accordingly. The spectral changes for the simple two-frequency exchange case, in which only the genuine double (C=C) and single (C-C) bond frequencies are taken into account, were formulated many years ago [10,11]. In case the CC frequency takes the double-bond frequency most of the time and only rarely jumps into the single-bond frequency, the following simple relations hold [9];
where W1 is the frequency of the collision with the solvent and t is the mean phase shift of the vibration (in the present case negative) which represents the most likely value of the phase shift associated with one collision.
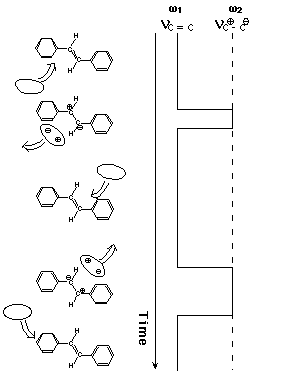
Fig. 3. Dynamic polarization model of vibrational dephasing in the olefinic CC stretch vibration of S1 trans-stilbene. For simplicity, two-frequency exchange scheme between ω1 (double-bond frequency) and ω2 (single-bond frequency) is shown. Note that the olefinic CC stretch frequency hops to and fro between ω1 and ω2 with the solvent fluctuation.
Just after the photoexcitation, S1 tSB is hot; the excess energy is shared with S1 tSB itself and the surrounding solvent molecules in the first coordination sphere. Then, the system cools down in the time range of 20 ps. As the temperature of the system decreases, the collision frequency decreases and hence ΔΩ and ΔΓ decreases. A decrease of a negative value of ΔΩ results in a shift to higher frequency. Furthermore, the primary effect of temperature is to change the collision frequency W1 and the mean phase shift t is likely to remain unchanged in a small temperature range. Then, Eq. (1) indicates that ΔΩ and ΔΓ change with temperature while keeping the ratio ΔΩ/ΔΓ=1/2t constant. Thus, Eq. (1) accounts very well for the observed time (temperature) dependent spectral changes of S1 tSB. It was shown recently that the concepts of the collision frequency W1 and the mean phase shift t in the simple two-frequency regime can be transferred, at least partially, to the more general case of dynamic polarization [9].
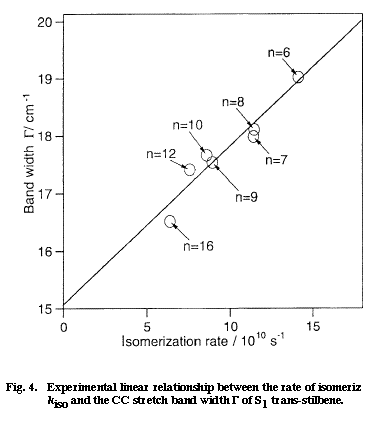
Fig. 4
Next, we want to understand the reason why the CC stretch band shape changes also with the solvent. Here, we come across with the very important question of the solvent dependent rate of isomerization of S1 tSB. It is well established by time-resolved fluorescence spectroscopy that the lifetime of S1 tSB changes markedly with solvent; in alkanes, the lifetime changes from 70 ps in hexane to 130 ps in dodecane. The solvent dependent lifetime of S1 tSB has been attributed to the change of the rate of the trans to perpendicular isomerization. Figure 4 shows a plot of the rate of isomerization kiso vs the band width &Gamma measured in seven different alkanes. There is a clear linear relationship between the two quantities which otherwise do not appear to be intrinsically correlated. As already mentioned, a linear ΔΩ /ΔΓ relationship holds for solvent dependent spectral changes. Therefore the mean phase shift t in Eq. (1) can be regarded as constant for seven alkanes. Then, the change in the band width ΔΓ is simply proportional to W1 and the kiso/ΔΓ linear relationship is transferred to the kiso/W1 linear relationship. Thus, according to the dynamic polarization model, the rate of isomerization is proportional to the frequency of the collision that dephases the CC stretch vibration. This relation seems to be sound because the rotation around the olefinic CC bond never takes place without disturbing the phase of the CC stretch vibration.
We model the trans to perpendicular isomerization of S1 tSB as in Figure 5, where we assume the participation of the second excited singlet state Z which is likely to be zwitter ionic [12]. By collision with the solvent (more generally, by the fluctuation of the solvent field), the Z state suddenly becomes lower in energy than the S1 state and the double-bond frequency jumps to the single-bond frequency. In this modeling, the dynamic polarization of the olefinic CC bond is schematized as the solvent induced non-adiabatic potential crossing from the S1 to the Z state. If the molecules stays on the Z potential surface long enough for evolution to the perpendicular configuration, the isomerization takes place. If, on the other hand, the duration and/or the strength of collision is not large enough, the molecule comes back to the S1 state and so does the CC frequency. Note that even with these weak collisions, the phase of the vibration is altered. The total isomerization rate is expressed as the product of the collision frequency W1 and the branching ratio W3/(W2+W3),
where W2 is the rate of the back hopping from the Z to the S1 state and W3 is the rate for the evolution on the Z potential surface. The experimental kiso/W1 linear relationship is well accounted for by assuming that the branching ratio W3/W2+W3) is almost constant for seven alkanes.
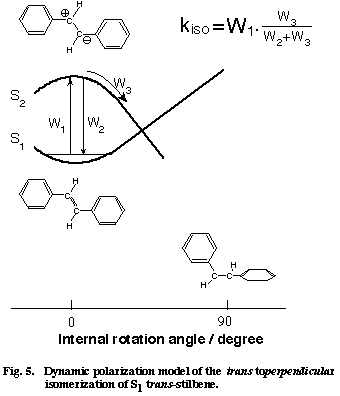
Fig. 5
Finally, we compare Eq. (2) with the conventional Arrhenius formula. It is straightforward to consider W1 as the pre-exponential factor of the Arrhenius formula. Then, the branching ratio W3/(W2+W3) corresponds to the exponential factor. The experimentally determined branching ratio in alkanes is 3.1×10-3, which can be rewritten in the form of the exponential factor at T=300 K with the potential barrier DE of 3.4 kcal mol-1. This value agrees excellently with the DE value (3.5 kcal mol-1) determined from fluorescence lifetime [12]. There is a certain formalistic similarity between Eq. (2) and the Arrhenius formula. It seems that the dynamic polarization model is a time-domain equivalent of the well established Arrhenius formula. Thus, picosecond time-resolved Raman spectroscopy has brought in a new view on the isomerization mechanism of S1 tSB in solution.
3. Picosecond time-frequency two-dimensional multiplex CARS spectroscopy
By combining the broadband multiplex CARS technique [13] with a high-speed streak camera, we are able to perform time-frequency two-dimensional (2-D) multiplex CARS spectroscopy [14]. This technique measures a set of picosecond time-resolved CARS spectra in the form of a time-frequency two dimensional image of CARS signal. It takes only hundreds of seconds to obtain about 20 picosecond CARS spectra with 15 picosecond time resolution. The data acquisition time is one hundredth of that needed by the conventional scanning CARS technique.
Diphenylacetylene (DPA) is known for its extraordinary photophysics, which are thought to be caused by strong interactions of closely lying excited singlet states with the environments [15-18]. In rare gas matrices, a clear mirror-image relationship between the ultraviolet absorption and fluorescence spectra was found, indicating that the emission originates from the excited singlet state to which the absorption terminates [16]. On the basis of the Kasha rule, it was thought that the emitting state was the S1 state. In solution, three transient absorption bands with different lifetimes were observed [17]. They were assigned to the S2 -Sn transition, the S1-Sn transition, and the T1-Tn transition, respectively. The fluorescence lifetime agreed with the lifetime of the S2-Sn absorption. Thus, in solution, the emitting state is not the S1 state but the S2 state. In order to fill the gap between the photophysics in matrices and solution, Ferrante et al. proposed a scheme which was based on empirical molecular orbital calculations [18]. According to their scheme, the ground-state absorption is assigned to the S0(A1g)-S2(B1u) transition. Internal conversion takes place in solution and the S1(Au) state is formed. In matrices, however, internal conversion is somehow prohibited and the B1u state is practically the lowest excited singlet state. Why such different photophysics apply to solution and matrices? In order to answer this question, we need the knowledge on the structure and dynamics of the excited states of DPA. We used our 2-D CARS technique to obtain the CARS spectra of these excited states [19]. The application of spontaneous Raman spectroscopy is prohibitively difficult because of strong fluorescence [20].
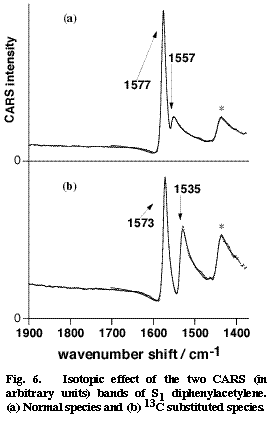
Fig. 6
Picosecond time-resolved CARS spectra of DPA in the S2 and S1 states have been obtained in cyclohexane [19]. The central CC stretch band of S2 DPA was observed at 2099 cm-1. This frequency indicates a triple bond character of the central CC bond in a linear acetylene structure. On the other hand, no S1 CARS band was found in the triple-bond stretch region. In stead, two S1 CARS bands were observed around 1550 cm-1. On the expectation that these bands might be assignable to the central CC stretch mode, we examined the 13C isotope effect by synthesizing DPA-13C in which one of the two central carbons is replaced with 13C. The results are shown in Figure 6. Upon the 13C substitution, the two bands at 1577 and 1557 cm-1 shift to 1573 and 1535 cm-1. These marked isotope effects are signatures of the two bands being contributed significantly by the central CC stretch motion. In order to analyze the isotope shifts quantitatively, we carried out a simple two-mode normal coordinate calculation that takes the central CC stretch mode and another ring mode into account. The calculation reproduced the observed isotope shift very well and gave the intrinsic CC stretch frequency of 1567 cm-1 [19]. Thus, the CC stretch frequency of S1 DPA has been obtained as 1567 cm-1, which suggests a double bond character of the central CC bond. This very low CC frequency is in good harmony with a quantum chemical calculation that predicted an extraordinary long CC bond distance for the S1 state [18].
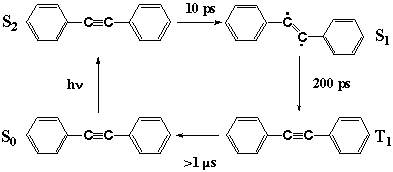
Fig. 7
With structural information from CARS spectra in mind, we can now discuss the unusual photophysics of DPA as in Figure 7. The photoexcitation of S0 DPA generates S2 DPA with a linear acetylene structure. In solution, intersystem crossing takes place in 10 ps and S1 DPA is formed. The structure of S1 DPA is likely to be a bent ethylene form. The reason why is manifold. First, the CARS evidence shows that the CC bond is a double bond rather than a triple bond. Second, in the prototype molecule acetylene, the S1 state having the same Au symmetry takes a bent structure [21]. Third, internal conversion in matrices is prohibited suggesting that the process is accompanied by a large structural change; simple CC bond elongation does not seem to be prohibitive in matrices. The S2-S1 internal conversion seems to be a linear to bent isomerization which causes the unusual dependence of the photophysics of DPA on the environments. More direct structural information, perhaps by infrared spectroscopy, is necessary to finally confirm the bent structure of S1 DPA. By intersystem crossing, the S1 state is converted in 200 ps to the T1 state, which is known to take a linear acetylene structure [20].
4. Nanosecond time-resolved dispersive infrared spectroscopy
An ultrasensitive nanosecond time-resolved infrared spectrometer has been constructed based on a dispersive infrared spectrometer and a high-speed MCT detector that is AC coupled to a low-noise broad-band amplifier. It can detect an infrared intensity change as small as one part in a million [22]. This detectivity is more than two orders of magnitude better than the conventional FT-IR method. Time-resolution is only limited by the detector response time which is 50 ns for a presently available photovoltaic MCT.
4-(dimethylamino)benzonitrile (DMABN) is another well-known molecule of high photophysical and photochemical significance. Since the proposal of the twisted intramolecular charge transfer (TICT) structure by Grabowski, numerous spectroscopic studies were reported on DMABN and related compounds [23]. However, no direct evidence for the twisted structure has so far been obtained. We used the nanosecond dispersive infrared technique and obtained the first infrared spectra of DMABN in its excited states [24].
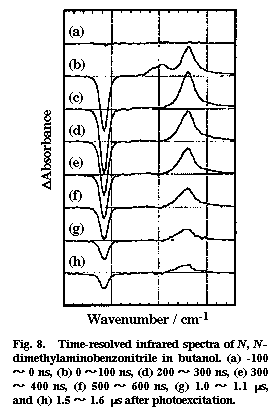
Fig. 8
Time-resolved infrared spectra were recorded for photoexcited DMABN in a polar solvent butanol and in a non-polar solvent hexane. Two transient bands were observed in butanol, whereas only one transient was found in hexane. Figure 8 shows the time-resolved infrared absorption spectra of DMABN in butanol. Two positive peaks at 2096 and 2040 cm-1 and one negative peak at 2216 cm-1 are found in the 0-100 ns spectrum. The positive peaks correspond to the increased absorptions due to the photogenerated transient species and the negative peak to the depletion of the ground state. The 2040 cm-1 band has a much longer lifetime than the 2096 cm-1. Oxygen quenches the 2040 cm-1 band very efficiently but does not affect much the 2096 cm-1 band. From these observations, we assign the 2040 cm-1 band to the CN stretch mode of the CT triplet state and the 2096 cm-1 band to the same mode of the CT singlet state. The only band observed in hexane (∼2000 cm-1) showed a strong oxygen effect and was attributed to the non-CT triplet state. There are a few implications concerning the structure of the CT singlet state. First, the frequency 2096 cm-1 is close to the CN stretch frequency of the benzonitrile anion radical (2093 cm-1). This agreement is consistent with the CT structure in which an electron is transferred from the dimethylamino group to the benzonitrile moiety. Second, the down shift of 120 cm-1 from the ground state indicates that the transferred electron flows significantly into the anti-bonding orbital of the CN group, contrary to what has been believed. Third, the estimated absorption cross section of the 2096 cm-1 band is 8.5 times as large as that of the ground state band. This large cross section means a large change of the dipole moment with the CN stretch vibration in the CT singlet state. It seems that the CT structure is dynamic and the transferred electron can move back and forth between the benzine ring and the CN group as the CN bond length changes with vibration. Fourth, time-resolved infrared measurements in butanol/hexadecane mixed solvents showed that the CN stretch frequency changes markedly with the solvent polarity [25]. This finding seems to suggest that, in a less polar environment, the electron transfer is only partial and that the electron is delocalized in the whole DMABN molecule rather than it is localized on the benzonitrile moiety. The idea of partial charge transfer is more consistent with the non-twisted structure of the CT singlet state of DMABN.
Time-resolved infrared measurements in the fingerprint region was also attempted but no reliable spectra have so far been obtained. Observation of the frequency of the ring-dimethylamino stretch mode will be a key to solve the structural problem of DMABN CT excited states.
Acknowledgment
I would like to thank Drs. C. Kato, K. Iwata, T. Tahara, T. Ishibashi, T. Yuzawa, M. Hashimoto, and S. Yamaguchi for their collaboration in the work described here.
References
- H. Hamaguchi (1987) Vibrational Spectra and Structure 16, 227.
- H. Hamaguchi,T. L. Gustafson (1994) Annu. Rev. Phys. Chem. 45, 593.
- K. Iwata, S. Yamaguchi, H. Hamaguchi (1993) Rev. Sci. Instru. 64, 2140.
- K. Iwata, H. Hamaguchi (1997) J. Phys. Chem. 106, 11.
- R. E. Hester, P. Matousek, J. N. Moore, A. W. Parker, W. T. Toner, M. Towire (1993) Chem. Phys. Lett. 208, 471.
- K. Iwata, H. Hamaguchi (1997) unpublished work.
- H. Hamaguchi, K. Iwata (1993) Chem. Phys. Lett. 208, 465.
- V. Deckart, K. Iwata, H. Hamaguchi (1996) J. Photochem. Photobiol.102, 35.
- H. Hamaguchi (1996) Mol. Phys. 88, 463.
- P. W. Anderson (1954) J. Phys. Soc. Japan, 9, 316.
- R. M. Shelby, C. B. Harris, P. A. Cornelius (1979) J. Chem. Pys. 70, 34.
- S. K. Kim, S. H. Courtney, G. R. Fleming (1989) Chem. Phys. Lett.159, 543.
- B. N. Toleutaev, T. Tahara, H. Hamaguchi (1994) Appl. Phys. B, 50, 369.
- T. Tahara abd H. Hamaguchi (1994) Rev. Sci. Instru. 65, 3332.
- K. Okuyama, T. Hasegawa, M. Ito, N. Mikami (1984) J. Phys. Chem. 88, 1711 (1984).
- M. Gutmann, M. Gudipati, P. -F. Scoenzart, G. Hohlneicher (1992) J. Phys. Chem. 96, 2433.
- Y. Hirata, T. Okada, N. Mataga, T. Nomoto (1992) J. Phys. Chem.96, 6559.
- C. Ferrante, U. Kensy, B. Dick (1993) J. Phys. Chem. 97, 13457.
- T. Ishibashi and H. Hamaguchi (1998) J. Phys. Chem. 102, 2263.
- H. Hiura, H. Takahashi (1992) J. Phys. Chem. 96, 8909.
- C. K. Ingold, G. W. King (1953) J. Chem. Soc. 2725.
- T. Yuzawa, C. Kato, M. W. George and H. Hamaguchi (1994) Appl. Spectrosc. 48, 684.
- Z. Grabowski (1993) Pure Appl. Chem. 65, 1751.
- M. Hashimoto and H. Hamaguchi (1995) J. Phys. Chem. 99, 7875.
- M. Hashimoto and H. Hamaguchi, unpublished work.